Annals of Robotics and Automation
Modeling, mechanics and experimental investigation of perpetual vibration of serial-chain direct-drive flexible robotic system
Debanik Roy*
Cite this as
Roy D (2024) Modeling, mechanics and experimental investigation of perpetual vibration of serial-chain direct-drive flexible robotic system. Ann Robot Automation 8(1): 008-029. DOI: 10.17352/ara.000018Copyright
© 2024 Roy D. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.The domain of Flexible Robotic Systems (FRS) is an exciting ensemble of global robotics research of the present decade, which unfurls various real-time data like rheology, vibration, sensor fusion, and non-linear coupled dynamics for control. As some of these features, especially strain-induced deflection and vibration, are inherent in FRS, the design and prototype development of multiple degrees-of-freedom flexible robots is highly challenging. The paper addresses the aforementioned design paradigms of FRS through logical understanding by giving importance to the manufacturable design-variables. Further, these design issues for the firmware of higher-order FRS have been explained with a focus on the novel design and hardware development of a prototype multi-link serial-chain FRS fitted with a miniaturized gripper at the free end. Besides hardware realization, the paper brings out an interesting feature in experimental robotics, namely, the evaluation of the natural frequency of vibration of a flexible manipulator using real-time data on dynamic strain produced within its body. This niche methodology gets propelled by the data from multiple strain-detecting sensors placed judiciously over the links of the FRS. Guided by this lemma, a novel theoretical analysis of the optimal placement of strain-sensors over the external surface of the FRS is described. Additionally, the paper dwells on a novel scheme for dynamic analysis as well as control system logic for the developed FRS. This research provides a complete canvas of design, modeling, firmware development, and experimental ab initio evaluation of perpetual in-situ vibration of a typical serial-chain FRS.
Introduction
Systems modeling in real-time and its realization through hardware have become instrumental in the performance assessment of Flexible Robotic Systems (FRS) in the recent past. A robust firmware of FRS is thus very challenging; especially when we attempt to fabricate multi-link FRS having resigned redundancy in terms of its degrees-of-freedom. It is prudent here to say that system rheology (stress-strain paradigms), in-situ vibration, sensor fusion, and non-linear coupled dynamics are heavily interlinked in the extended envelope of flexible robot research. Time-spanned quantification as well as characterization of all these factors for real-time control of FRS is undoubtedly a challenging domain as the application of FRS is slowly wide-spreading in several social systems, medical and para-medical diagnosis, and healthcare.
Although flexible robots have become a favourable choice in several new applications because of their slender design, light weight, small size envelope, and increased reachability in the workspace, the major bottleneck of FRS lies with the effective control of its built-in vibration. This structure-independent inherent vibration gets realized in the form of mild to severe trembling of the slender links and/or shaking or twisting of the inter-spaced joints, no matter what the type of FRS-hardware is. In fact, the slenderness of the links as well as the design of the FRS joints does play an important role in the self-generation of this trembling. As observed in the FRS-hardware, internal stress-strain and vibration (modal frequency and eigenvalue) are completely built-in types and hence those are design invariant.
Several designs of FRS have been attempted by the researchers in past decade to alleviate this vibration but most of those trials have been unsuccessful. The problem gets even more complicated when we attempt for multi-link design of the FRS, wherein various kinds of coupled effects and non-linearity crave in. It has been also observed that vibration in FRS is not time-dependent and the duration and periodicity of it can’t be correlated with the task-space of the robotic system. Besides, this vibration is self-propagating in nature as well as random and it gets induced to the successive member of the FRS till the end-link and end-effector/gripper. So, we must have a real-time assessment of vibration signature in FRS a-priori towards establishing a reliable application-centric control system.
It may be mentioned that a significant share of research in hardware development of FRS catered to only the manipulator hitherto by neglecting the important member of such system, namely tts gripper/end-effector. This has become a serious lacuna because no proper estimation of the run-time performance (e.g. grasping) of such FRS can be adjudged apriori. In fact, experimentations on the run-time performance of a typical multi-degrees-of-freedom FRS must necessarily include field trials on the graspability and maneuverability under unknown and/or unstructured environments. We wished to address this shortcoming of the research on FRS, by proposing a working model for the evaluation of natural frequencies of vibration (both fundamental as well as modal) through strain sensor data. In order to fulfill this niche objective, the four verticals of FRS-research, namely bi-planar rheology, non-linear coupled dynamics, modalities of perpetual vibration, and fusion rule-bases for sensor data have been orchestrated synergistically in the present work.
A new model on vibration-induced dynamics of the multiple degrees-of-freedom FRS is reported in this paper. The vibration signature in such FRS gets assessed in real-time through various force sensors, affixed over its links and joints in a geometrical layout. A majority of the dynamic models used hitherto in FRS have been found to be somewhat inappropriate for real-time monitoring and control of the end-of-arm payload. We will discuss a novel dynamic model of the multi-link FRS in this paper, referring to its real-time operation.
Control issues of FRS have gained research attention over the last few decades that deal with novel techniques for harnessing system dynamics in real-time [1]. While the perturbation method was tried for fine-tuning the FRS controller [2], direct real-time feedback from strain gauges was experimented too [3]. A robust dynamic model indeed becomes very effective in understanding the behavior of FRS in real-time and the same becomes crucial for a multi-link FRS [4,5]. Feliu, et al. attempted the control issue of a three degrees-of-freedom FRS using the methodology of inverse dynamics in contrast to strain gauge-based control [6,7]. The fuzzy learning-based approach for the control of FRS was also reported by Moudgal, et al. [8]. Specific metrics related to the reduction of system vibration of a robotic gadget were attributed by Singer and Seering [9]. Various techniques for vibration attenuation and control in FRS have been reported hitherto, such as sliding mode theory [10], adaptive resonant control [11], online frequency and damping estimation [12], and integral resonant control [13]. Dynamic model and simulation of FRS based on spring and rigid bodies was established too [14].
It is important to comment here that laboratory-based experimentation on the control semantics of single-link flexible robots gained substantial leverage over the years. These flexible arms have served as robust test-bed for various new control strategies like load-adaptive control (using end-of-arm mass) [15,16]; end-point control [17]; acceleration-feedback control [18] and inversion method-based trajectory control [19].
A chronological survey on FRS research reveals that nearly all global studies hitherto are concentrated on various experiments on the control synthesis of single-arm FRS with or without end-mass. The kinematic and dynamic effect of end-of-arm tooling and/or gripper in such FRS has also not been addressed to date. However, both rheology and vibration characteristics of FRS will drastically alter as soon as a jointed structure is in place, i.e. multi-link multi-jointed FRS with a miniaturized gripper fitted at the open end. We have investigated such scenarios of control dynamics for a multi-degrees-of-freedom FRS fitted with a mini-gripper [20], postulating spring-dashpot-based model (for vibration signature) and strain gauge-induced model (for dynamic strain signature). Design of the drive and actuator system for a test set-up of a three-link serial-chain FRS and subsequently, a realization of its firmware has been reported by the author’s group [21,22]. The proposition of real-time vibration signature of planar FRS and its harnessing has been discussed thoroughly by the author [23]. Tang, et al. [24] investigated a nice problem of vibration signature as well as its natural suppression, as obtainable in a flexible robot. Likewise, theoretical postulation leading to improved dynamic models of a typical FRS and experimental validation of those was made for the design of the control system [25] as well as real-time control of a flexible robot using harmonic functions [26]. Several researchers have put forward significant mathematical insight into the dynamic model of a flexible robot through the pathway of advanced finite element analysis. For example, the influence of non-linear modeling in transient dynamic analysis of FRS was studied by using standard beam-element of finite element analysis [27]. Nonetheless, in order to undertake deep-rooted studies in dynamic analysis, novel spatially translating and rotating beam finite elements have evolved for the said modeling of FRS [28].In general, adopting systematic procedures is the pre-condition for any successful dynamic modeling task for a flexible robot ~ a glimpse of which is reported by Li and Sankar [29]. The run-time dynamic characteristics of a two-link flexible manipulator do have certain complexities in comparison to that of a uni-link flexible manipulator when subjected to a set of pre-conditions on its workspace [30].
Dynamic model and control theologies of multi-link FRS are indeed relatively more complex than their counterparts for uni-link flexible manipulators. For example, modeling paradigms in the domain of multi-link flexible manipulators made up of prismatic joints were studied [31], followed by the development of control semantics of multi-link FRS by the authors [32]. The mathematical modeling of the oscillation dynamics as well as its semi-spiral trajectories pertaining to a multi-jointed FRS has been reported by the author in the recent past [33]. The facets of perpetual vibration under natural conditions of operation for a single-link flexible manipulator have been modeled by Rao, et al. [34] that involve novel mathematical tools, e.g. fuzzy mathematics, for obtaining the final posture of the FRS under an uncertain environment of operation.
The paper has been organized into six sections. An overview of some critical design variations and mechanical sub-assemblies of the serial-chain FRS is presented in the next section. Details on the sensory augmentation and modeling of the control dynamics of the developed FRS have been discussed in section 3. Salient aspects of the hardware of the fabricated FRS are reported in section 4. Section 5 addresses the paradigms of the control system algorithm, an overview of the FRS-controller developed, and test results. Finally, section 6 concludes the paper.
Critical design facets and mechanical sub-assemblies of serial-chain flexible robot
Out of various design paradigms of serial-chain FRS, three facets are considered to be critical, which are instrumental in finalizing the overall design ensemble of the FRS as well as its manufacturing. These three critical design facets are: a] cross-section of the link:{circular; rectangular; square}; b] design morphology of the slender link::external metrics {straight; tapered and stepped-section} and c] end-of-arm attachment: {tip-mass; end-effector; mini-gripper}. It is prudent to note here that vibration and/or rheological features of the FRS do alter under two situations of end-of-arm attachment, viz. end-/tip-mass vis-à-vis a mini-gripper (at the distal link of the FRS). Figure 1 schematically illustrates the critical design facets of a typical serial-chain FRS with uniformly varying tapered cross-sections, as stated in [a] and [b] earlier. Three types of possible cross-sections of the FRS-links, namely, circular, rectangular, and square, are shown in Figure 1a, b, and c respectively for a single-link FRS-arm. The cross-sections are detailed under section A-A’. Cartesian co-ordinates are established at the ends of the ith. FRS-link, viz. at two joint locations (Ji-1 and Ji), spanning a horizontal length Li and an inclination of {qi}k (a measure of flexibility at the kth. vertical plane). The measure of taper is being indexed as {ci}k at the kth. vertical plane. It is important to note also the numerical measure of the cross-sectional area of the ith. FRS-link at pth. section, Di, based on its type, viz. radius ‘r’, length ‘l’ and breadth ‘b’ tuple and side’s’, respectively for circular, rectangular, and square cross-sections. Although Figure 1 is pictorially explicit for a single-arm FRS, the same nomenclature will be valid for multi-link FRS too.
Irrespective of the type of cross-section of the FRS-link, we need to focus on the external design morphology to factor out the effect of in-situ vibration of the FRS during its operation. Here, the sub-group, straight can be conceptualized as a special case of tapered type with uniform cross-section throughout. Likewise, the stepped type link is another modification of the tapered type. The common features of these designs are i] variation of link cross-section at different transverse sections, e.g. section [A-A’]p (with sectional area: [Di]p ) and ii] variation in link inclination as ‘instantaneous measure of flexibility’ at different locations of the link, e.g. {c}ik. Mathematically, for tapered N-link FRS we can state these paradigms using two proportionality constants, viz. x and l. The first set of the model involves cross-sectional area, as shown below:
and
Where LA-A’ signifies the length of the link from Ji-1 to the location of the A-A’ section-plane and ‘q’ denotes any intermediate location on the link. While eqns. 1 and 2 are related to the variations in cross-sectional area for each link of the FRS due to tapering, next two equations are related to link inclination.
and,
It is important to figure out the overall inclination of the serial-chain FRS (having ‘N’ links) at a particular time-instant. The gross inclination (drooping) of N-link FRS can be modeled as:
where, <θ>FRSt signifies the overall drooping of the FRS at time ‘t’, which is numerically equal to the maximum of the inclinations of the individual links.
It may be noted that the equations, stated so far, viz. eqn. (1) to (5) are novel and evolved ab initio, by considering the design semantics of the FRS with the basics of physics. The propositions, so framed, are the original conceptualization of the author.
The inherent trembling of the FRS-links and subsequently, the deflection/drooping of the links is the prime-most factor from a control system standpoint. Figure 2 schematically depicts such in-situ deflection of FRS-links, wherein all joints of the two-link serial-chain FRS are actuated through direct-drive. It may be pointed out here that direct-drive FRS needs a special layout of its revolute joint(s), primarily due to the slenderness of the system and also partly due to the placement of the motor. The schematic of Figure 2 as a whole and the artistic disposition of ‘J2’ in particular help conceptualize this special design metric of the revolute joint. We shall deliberate on this specific design later in this section.
We may infer from Figure 2 that one of the crucial aspects of FRS-design pertains to the choice of drive mechanism. In the present prototype hardware, we have adopted a direct-drive approach, wherein miniature servomotors were placed at the joint itself. Direct-drive-based design is more realistic and comparatively robust from the point of view of system actuation but it suffers from poor vibration control. As the system tare weight is increased due to the addition of servomotors at the link-joint interface, the trembling or in-situ vibration becomes more prominent in the case of direct-drive FRS.
Figure 3 presents an ensemble schematic of the developed small-sized serial-chain direct-drive FRS hardware, having three links and three joints in between. Hence, the overall span of an n-link FRS in Figure 3 is indexed as ‘SLi’, where link lengths are denoted by ‘Li’, ∀i = 1,2,3,…,n. Likewise, the revolute joint-ensemble is indexed as {Ji, Ji+1, Ji+2,…..,Ji+n-1} when a fixed value of ‘i’ is considered (i=1). However, servomotor-ensemble is indexed as {Mi-1, Mi, Mi+1,….,Mi+n-1}, under i=1. The special disposition of the intermediate joints, viz. ‘J(i+1) and ‘J(i+2)’ may be seen in detail for the characteristic layout of the revolute joints of the demonstrable hardware.
It is important to note here that the ensemble modeling of the prototype FRS, as described in Figures 1,2, have been done with respect to the local coordinate system, maintaining a Cartesian frame of reference. Although the global reference system has been attributed to the base of the FRS, it merely serves the purpose of the overall disposition layout of the FRS. The governing design-eqns., as presented in eqns. 1 to 5, are fundamental in nature and those do follow a local coordinate system under the Newtonian frame of reference. For example, eqn 4 is framed up under a local coordinate system for the ith. FRS-link, wherein we have investigated the variation in the angle of inclination at different cross-sections within the link [viz. sth. and (s+1)th. sections].
The drive for all three joints is direct, i.e. coupled straight away with the respective servomotors. The mini-gripper, E is being actuated through its dedicated servomotor, Mg, located at the backside of the gripper baseplate. The system is to be mounted on a customized mechanism beneath the base, having translational motion to position the FRS at the desired horizontal plane. The mechanism is composed of two sub-assemblies, viz, tripod stand, B1, and prismatic slide, B2, driven by motor M0. This prismatic slide is positioned on the tripod and is being actuated through a re-circulating ball screw–nut mechanism having linear movements along the vertical Z-axis. It may be noted here that we have described the gripper coordinate system in the local reference frame, so as to bring parity with the rest of the local Cartesian frames earmarked for the FRS-links. Nonetheless, the gripper/tool center point can be re-calculated through the system of orthogonality and also by means of forward kinematics routine (D-H matrix) with respect to the global (absolute) frame of reference (X i-1, Y i-1, Z i-1).
A salient paradigm of a serial-chain FRS pertains to the optimal joint design. Serial-chain FRS being planar, all joints are ideally conceived as revolute type, with design variations in its sub-assemblies. Essentially, these revolute joints are different incarnations of simple ‘pin-joint’, but at different working planes (depending upon the layout of the FRS). Barring minor design variations, all FRS joints have rotating shafts, miniature ball bearings, end-covers, housing, and at times, a gear-train (worm-worm wheel or spur). A realistic and perfect design of an FRS-joint begins with the layout disposition of various constituent members of the joint assembly, viz. joint-body, coupler, gear-train, servomotor, and finally, the plane of the joint actuation and the direction of assembly/disassembly. The conceptualization of the actuating plane of the FRS joint is the prime-most criterion of a successful joint design, which can be either along the horizontal or vertical plane. Figure 4 schematically illustrates the layout disposition of a typical revolute joint of a serial-chain FRS.
It may be pointed out that our customized and novel design of the revolute joint has its rotary motion in the horizontal plane, which is a deviation from the usual form of rotary motion along the vertical plane. This altered disposition is essentially need-driven, in order to tackle the tinyness of the joint after the miniature servomotor gets fitted in. Although the concept of servomotor-gearbox assembly remains unchanged, the physical fitting of the said assembly has been made in the X-Y plane, rather than the usual Y-Z or X-Z plane. Thus, the assembly as well as disassembly procedure of this novel joint is quite different from the standard one and it needs care in handling the joint sub-systems, especially the coupler.
Joint design and joint assembly thereof are correlated to the design of links too as the end-fittings of the link(s) will be an extended part of the joint assembly. This link-joint mating zone is very significant in FRS, unlike the usual serial-chain robotic manipulator. The labeled schematic of the revolute joint assembly of a serial-chain FRS is shown in Figure 5, highlighting the salient dimensions of the constituent members. The crux of the design of our revolute joint is the central pin~ the axis of the joint assembly. This pin is supported by two sets of miniature ball bearings. The pin is subsumed in a custom-built casing that can be opened up in two parts for easy assembly and disassembly. These two mating parts of the casing, namely the top and bottom casings, are dovetailed with each other through precision machining.
With this design backdrop, we can locate the main element of the joint assembly in Figure 5, which is the centrally-located pin, having a diameter ‘d’. As illustrated in Figure 5, this pin is supported by a pair of miniaturized ball bearings (diameter: Dbr), disposed off symmetrically with respect to the pin, one above another. The intermediate space between the bearings, Hj is dimensionally crucial, as actuating links will be positioned in this space. The top casing of the pin is disposed of along both sides of the pin as a single unit. The important design dimensions of the top casing are width (Lt) and height on either side (Ht and Hts). In contrast to the top casing, the bottom one is fabricated as a single unit, encapsulating the central pin. The crucial design dimensions of the bottom casing are width (Lb) and height on either side (Hb and Hbs).
The housing of the FRS joint is another important member of the entire joint assembly. The assembly-handshaking between the actuating links as well as the pin-joint ensemble is crucial dimensionally. Besides, close tolerance needs to be maintained to achieve the reliability of the joint assembly while in motion. The external sectional view of an assembled joint housing is illustrated in Figure 6.
As can be seen from the housing design of the FRS-joint in Figure 6, the first and foremost decisive feature is the link diameters, namely, DLi and DL(i+1), corresponding to the two successive links of the FRS that are being joined. The mating of the links under close push fit will be decided by the inter-bearing distance (Hj: refer Figure 5). The joint housing is designed with respect to the consideration for width (W1 and W2) as well as height on either side of the pin joint assembly (HL and HR) and finally the radius of the detachable dome atop (RH). The joint assembly has easy access for service and maintenance from the top of the housing, as shown in Figure 6.
The present prototype FRS has the following four sub-assemblies, viz. a] Base; b] Link and Joints; c] Mini-gripper, and d] Drive system and controller. The base sub-assembly is a novel mechanism that has interconnection with the first link and system controller (refer to Figure 3). The prismatic movement helps the FRS to achieve the desired planar location depending on the end application. The link and joint sub-assembly is the backbone of the prototype as it maintains the synergy between the link, actuating joint, and driving servomotor. The driver circuitry and motion controller of each servomotor, along with wiring and instrumentation were augmented under a separate ensemble, interfaced with the base sub-assembly.
Sensory input and modeling of the real-time dynamics for control of the flexible robot
A. Need, fitment and augmentation of sensor in FRS: The ensemble motion of any link of a flexible robot in real-time is a conglomeration of two entities, namely: a] rigid motion (similar to Euler formulation of rigid body dynamics) and b] elastic motion (description of the deformation state). While the rigid motion is characterized by the rheology of the FRS, e.g. strain vectors of the links/joints, the elastic motion serves as the source for the inherent vibration of the system.
It is to be noted that the inherent vibration of a flexible robot is directly proportional to the number of degrees of freedom of the FRS. We may also appreciate that basic strain in FRS-link is being measured through multiple strain gauges, placed over the external surface of the link(s). The paradigm of in-situ vibration of FRS-link can be symbolized optimally as the real-time deflection of a hollow beam having various cross-sections, as shown in Figure 7. The locations of placement of strain gauges have been marked by the ‘=’ symbol in four possible design variations (straight, stepped, circular, elliptical). The fulcrum location of the beam cross-section is denoted by ‘∆’. The engineering details of the strain gauge are provided in the left-hand-side panel of Figure 7.
As illustrated in Figure 7, the FRS member will have a micro-beam and the force-sensing mechanism will be based on the beam deflection principle. A particular FRS member may have multiple beams embedded in it, each having its own characterization. The placement of those beams inside the FRS member is also another technological challenge. In our case, tapered hollow cross-section circular links have been used for prototype fabrication, resembling the template layout of Figure 7c.
Each link of the prototype FRS is augmented with strain gauges and flexi-force sensors. Due to the constraint of hardware and allied logistics, we have limited the fitment of strain gauges in contrast to that shown in Figure 7c. As per design, 5 strain gauges and 2 flexi-force sensors have been fitted on each FRS-link. Hence we can say that the material-specific deformation of the FRS-member will act as the precursor for the sensory module of the prototype FRS. Strain gauge-type resistive sensors are the prime sources of detection of the vibration in FRS in real-time, backed up by indigenous electronic circuitry hardware. The semiconductor strain gauge (make: Entran Inc., model: ESB-020-350, resistance: 350 ohms) is used to detect and measure the in-situ deflection, as generated at the FRS-links. These strain gauges are exceptionally suitable for small load measurements and instantaneous forcing, such as touch, push, pull-type force, or any sort of impact force vector of short magnitude. Figure 7 illustrates the dimensioned view of the semiconductor strain gauge (enlarged view, not to scale) with external dimensions [the dimensions are in mm., with corresponding values in inches inside parentheses]. The flexi-force sensor that was used in the FRS hardware had a thickness of 0.203 mm. and a width of 7.6 mm., made up of polyester substrate. It has a very quick reception of strain/deflection/oscillation at the grasp zone (of the FRS-gripper) and we can get the desired amount of external load on the FRS-gripper.
B. Modeling of real-time dynamics of FRS for control: The flexible link of a serial-chain FRS can be conceptualized as a ‘free elastic body’ in an ideal scenario, but for all practical purposes, we can treat it as a ‘cantilevered elastic body’, which acts as the prime source of in-situ vibration of FRS. In all practical situations of serial-chain FRS, this inherent vibration is evaluated in terms of the natural frequency of vibration (wn) and the higher-order modal frequencies. The inherent vibration of FRS is directly proportional to its number of degrees of freedom. The study on the movement / instantaneous motion of FRS-links should ideally be restricted to low joint speeds, thereby neglecting the second-order effects of elastic deformation. In fact, in all such cases, second-order and higher terms of control equation need to be avoided for successful control of FRS. On the other hand, the dynamic strain vector (ei, ∀i = 1,2,3,…,k: where ‘k’ is the link number of FRS) is evaluated from structural analysis of the FRS. Thus, the paradigm of control dynamics of FRS in real-time essentially involves the investigation of strain vis-à-vis vibration tuple. In the case of ‘direct-to-joint-drive’ serial-chain FRS, the instantaneous real-time displacement, in the form of ‘deflection’, will be prudent in the links. It is important to note that an efficient dynamic model of FRS will be able to characterize the deformation and deflection of the FRS-members in real-time. While FRS links are more prone to deflection with a certain frequency of vibration, the joints are subjected to mild deformation. At times these two entities are quite inseparable and we need to reply on FEA simulation and trial-run of the hardware only.
If we take a closer look over the traditional dynamic equation of a rotational body involving inertia, damping, stiffness effect, and finally torque, then the same can be expanded for FRS too as shown below, which is the fundamental equation of real-time control of any robotic system par se:
In fact, eqn. 6 is self-explanatory wherein the parameters, ‘M’, ‘B’, ‘K’, ‘f’ and ‘t’ have their natural nomenclatures. For instance, ‘M’ is the mass moment/inertia of the system; ‘B’ is the viscous damping; ‘K’ is the spring constant of the naturally vibrating system; ‘f’ is the joint angle movement, and ‘t’ is the torque function. Now, let us take a deeper understanding of eqn. 6 and we will observe that it is essentially composed of two broad groups, viz. [a] Material-specific Equation and [b] Torque-specific Equation. We can appreciate that eqn. 6 is in the format of a Generalized Dynamic Equation of motion, namely,
Where ‘q’ signifies the joint variable in generalized co-ordinates. While the parameters pertaining to the material-specific equation move around the matrices of ‘M’, ‘B’, and ‘K’, the torque-specific equation gives weightage to the assimilation of various kinds of torque components appearing in FRS.
Let us now take an inlook into the expanded form of control dynamics equation of serial-chain FRS, by amalgamating eqns. 6 and 7 and inducing a few measurable parameters. We will treat the serial-chain FRS as an open-end cantilever structure, thereby imbibing spring-effects at the links and joints. Viscous damping will also be modeled as two metrics, located at the link and joint. This conjugate approach of modeling the spring constant and viscous damping has been used in order to ascertain the intricacies of the real-life actuation of the FRS.
The ensemble deformation at the FRS-joints will be accounted as friction torque while stiffness will be estimated through viscous damping of the joints as per the equation below in support of the real-time dynamics of the FRS:
Where, i: link number; p: joint index; Ji-1 and Ji: Consecutive revolute joints; q: Rotation of the link; M: Desired moment of inertia matrix of the link; Bi:Desired viscous damping (friction) coefficient of the ith. link; Bp: Desired viscous damping coefficient of the pth. joint; Kp: Desired stiffness of the pth. joint; for in-depth analysis of the twisting phenomena, comprising the twist of the joint and twist at the link-joint interface. The twist of the FRS links and joints is complex and it will involve modeling the stiffness in quadrature plane(s) at a particular time-instant. It may be noted that root - control system model, vide Ki: Desired stiffness of the ith. link; Kip: Desired stiffness of the Link-Joint Interface (ith. link and pth. Joint in mating condition); d: Initial angular position of the link and/or joint; tf: Frictional torque; tL: Load torque; N: Real numbers.
It may be observed that the proposed dynamic model of the FRS, as per eqn. 8, is essentially a torque-induced material equation, wherein the selection of appropriate material for the links as well as the joints is very crucial. The terms of the dynamic model equation include vectors of angular velocity and angular acceleration that need to be determined through real-time experiments. It is also interesting to note that we have bestowed importance on the characteristics of viscous damping and spring constant by augmenting the influence of both link and joint and finally, the link-joint interface. We can model the viscous damping coefficient of the joint and stiffness of the link-joint interface as shown below:
In contrast to eqn. 8, we may deduce the generalized expression for the Torque-specific Equation for the FRS as:
Where ‘F’ denotes the real-time function of ‘q’ and time-instant ‘t’, which is obtainable from the generalized terms of eqn. 6 or eqn. 8. Rest of the parameters and legends of eqn. 10 are identical to that of eqn. 8. Thus we can express F(q,t) for any link and link-joint combination as per the following expression, utilizing material-specific nomenclature of the FRS (viz. ‘a’, ‘b’, ‘l’):
At this point, it is worthwhile to mention that a complete dynamic model of the serial-chain FRS must incorporate both link and joint rotation as well as joint twist. While the paradigm of real-time rotation of link and/or joint will be tackled by the present model, vide eqns. 8-11, modeling of joint twist will call eqns.8 and 9 do not involve time function and thus the model is perfectly suited for joint flexure only.
Fabrication of prototype serial-chain flexible robotic system: Salient aspects
A. Paradigms: The working prototype of the serial-chain FRS was fabricated indigenously, equipped with three nos. revolute joint-actuated links of unequal length but uniform cross-section and one no. miniaturized gripper at the distal end. All revolute joints are actuated through D.C. servomotors (Make: Faulhaber™), integrated with a gearbox and encoder. The flexible robot is equipped with several limit switches for each servomotor in both directions so as to invoke precautionary measures for overrun of the rotary motions. The fabrication of the prototype FRS was realized through five sub-assemblies, namely: a] Fitment of the First Link and Base Sub-assembly; b] Second and Third Link Sub-assembly; c] Joint Sub-assemblies; d] Gripper Sub-assembly and e] Tripod Sub-assembly. It may be stated here that it was not possible to initiate the entire manufacturing of the FRS in one shot due to its long and slender disposition, piggy-backed with testing of motor controllers and strain gauge-based instrumentation. This piece-meal testing of the joint controller, sensory instrumentation, and gripper operation gave an edge over the final assembly of the FRS towards full-proofing the same. With reference to Figure 3, it may be noted that except for the base (tripod) sub-assembly, all other components and sub-assemblies are mostly hand-made. This is a unique feature of our prototype, especially for the miniaturized gripper. Another salient aspect of the prototype is its sleek wiring and cable-routing. Figure 8 shows the partial photographic view of the developed three-link serial-chain direct-drive flexible robot with the mini-gripper, in a thematically assembled disposition (two parts, viz. [I] and [II]: second and third links and mini-gripper:: to be seen from left to right). The relocation of the prototype FRS, post-commissioning, is not trivial as the assembly of the flexible robot needs to be compacted under 3 to 4 functional sub-assemblies, as indicated in Figure 8. The design for the second and third links of the prototype FRS was carried out with reduced lengths but without altering the uniformity in cross-section. The second link is half of the size of the first one, i.e., 400 mm. As an effect of in-situ vibration is ideally predominate in the first link, we have fitted only one strain gauge over the surface of the second link. The third link is the shortest; its length is 200 mm. only. No strain gauge is fitted on the third link because the ensemble vibration effect of the third link gets engulfed by that of the mini-gripper. Sub-assembly-wise detailed descriptions of the mechanical hardware of the prototype have been reported in the ‘Part I’ paper [76].
B. Critical sub-assemblies: Fabrication of the prototype serial-chain flexible robotic system comprises two critical sub-assemblies that need special mention. The joint sub-assembly is prime and most critical so far as its delicateness and precision are concerned. The other critical unit is the tripod sub-assembly, which is responsible for the actuation of the flexible robot in different X-Y planes, depending upon the need of the end-application. A majority of the other three sub-assemblies are hand-made types, which are largely skill-based.
The prototype FRS has been fabricated using two identical and inter-replaceable revolute joint assemblies. The first joint is located at the interface of the first and second links (link 1 and link 2) while the second joint is positioned in between the second and third link (link 2 and link 3). The novelty of the design of this joint system is related to its placement along the axis of suitability. Although it looks trivial in describing this sort of revolute joint, its manufacturing is quite tedious due to its tiny volume. Besides, CFRP-made joint-base is also delicate to handle, especially for drilling and fixing of fasteners. Figure 9 shows the photographic view of the indigenously manufactured revolute joints used in the prototype. These are placed respectively between link 1 and link 2 (‘joint 2) and between link 2 and link 3 (joint 3), as shown in Figures 9a,b.
So far as the tripod assembly is concerned, we have two important components that needed attention during assembly, viz. i] recirculating ball screw and ii] pair of customized spur gear, made of Fibre Reinforced Plastic (FRP). The ball screw gets assembled with its actuating motor at the bottom side of the tripod assembly through the pair of custom-made spur gears. The main issue of this fitment is the alignment and vertical positioning of the tie rods, associated with the ball screw –nut system (make: THK™). Figure 10 illustrates the photographic view of the tripod assembly of the fabricated FRS.
One of the novelties of the present prototype FRS lies with the judicious placement of the servo-drives and controller board of the D.C. servomotors, responsible for joint actuations. Because of the compact shape and size of these controller boards, we decided to mount the boards on the links, minimizing the volume and weight of such sub-assemblies. On-link fitment of these controller boards does make the direct-drive metric of the FRS-joints more pragmatic and useful, as the linear distance between the joint axis and the centroid of the controller board becomes the shortest. On-link fitment of the controller boards also helps harness the in-situ trembling of the FRS-links, because of the additional weight. The slender circular shape of the FRS-links facilitates easy routing of the cables, jutting out of the controller boards (refer to Figure 8a for details).
The unique custom-made design of the servo-controller board also facilitates connectivity with the servomotor at the joint and also with the sensory systems of the FRS. Two variants of multi-wire flat cables are used for these connections by using the screw terminal ends of the controller board. The wiring diagram and associated layout at screw terminals are customized to the extent of easy manual fitment. Figure 11 illustrates the zoomed view of the servo-controller board, highlighting the wiring connection for the servomotor as well as sensory systems of the FRS. The screw terminals are distributed on the left-hand and right-hand sides of the servo-controller board and are responsible for the wiring of the servomotor (refer to Figure 9b) and sensors respectively.
C. Fittment of sensors: The augmentation of sensors does play a significant role in the overall performance of the prototype FRS. While rheological data pertaining to strain and vibration of the FRS-links and joints have been captured by the semiconductor-type strain gauges, the instrumentation at the mini-gripper is attributed to the flexi-force sensor, mini-load cell, and infra-red sensors. Figure 12 shows the photographic view of the fixation and instrumentation of flexi-force sensors on the mini-gripper. The long and slender flexi-force sensors are mounted on the jaw-plates of the gripper, fitted with a sleek connector (refer to ‘C’), which is finally connected to the multi-wire cable for sensors (refer to ‘D’ of Figures 11,12). The servo-control board for the gripper motor is mounted on the flange part of the gripper body to reduce wiring as well as trembling of the gripper-body. The hardware augmentation of flexi-force sensors becomes critical predominantly due to the length, which becomes a constant source of jitter for the ensemble mini-gripper. The fitment of the infra-red sensors (as emitter and detector pair on both jaw-plates) is also challenging because of the tiny sizes and the space available for fixation (refer to ‘F’ in Figure 12). Both the fitments were skill-based and carried out manually under extreme care. On the contrary, fixation of strain gauges was relatively easier, although the tiny sizes did cause bottlenecks, throughout the assembly sequences of FRS-links.
Control system hardware of the flexible robotic system and test results
A. Overview of the control system algorithm of the FRS: It is important to note that designing the control system of a typical compliant/flexible robotic system or in that regard, any soft robotic system primarily depends on the augmentation of servomotor assemblies in the respective mechanical hardware. In that respect, the choice of the servomotor and the control sequences do vary based on the real-life hardware of the FRS. Physical placement of the prime-movers (e.g. servomotor assemblies) do depend heavily on the mechanical design architecture of the FRS, e.g. tensegrity-based structure [35], continuum manipulator [36,37] or soft robotic structure [38-40]. The crux of all such customized designs of the FRS controller is to unearth the potential of a low-power control unit that is capable of being synchronized with variable stiffness mechanism(s) inside the FRS [41]. Although inverse dynamics routine-based control algorithm finds its best application in trajectory control of robotic manipulators, the same may not be the most optimal choice for a flexible system due to the perpetual oscillations Nonetheless, custom-made tracking controllers can be a viable choice for semi-slender manipulators with low joint stiffness [42-45]. However, experimentally determined control semantics for a direct-drive robotic arm can perhaps be the closest associate for building up the same for a typical multi-degrees-of-freedom direct-drive FRS [46].
The backbone of the control system algorithm of the fabricated flexible robot is Proportional-Integral-Derivative (PID) control, augmented by a novel vibration (frequency) attenuation module. The overall control system facet has been tuned with current-based cut-offs and electronic limit switches to arrest joint overrun. The servo-based control of the FRS-joints as well as the FRS-gripper has been effected by individual user-selective feedback gain amplifier(s). Figure 13 presents the block diagram of the control system algorithm that has been invoked in the firmware of the prototype FRS.
It is to be noted that the control system architecture of the prototype FRS is composed of four distinct but similar PID loops, each one of which is responsible for the three joints of the FRS and the mini-gripper. The set-values of the joint-angles of the three revolute joints of the FRS, viz. j=1,2,3 play an important role in tuning the PID control-blocks thereafter. These set-values, {q1, q2, q3} are assigned a-priori through the dedicated servo-controllers (Make: Faulhaber®) of the corresponding servomotors of the joints. The program-code, generated for the FRS, includes these set-values and these values can be re-set depending upon the need of the end-use. Similar to the selection of the set-value triad of the joint-angles, the servomotor, responsible for the actuation of the mini-gripper of the FRS also gets tuned by setting the rotary motion of the motor-shaft of the FRS-gripper. Hence, the ensemble set-value of the FRS, [{q1, q2, q3], {qG}] becomes the maiden input to the system controller and its matching program-code.
The next step of the algorithm of the system controller is related to the tuning of the gains of the proportional, derivative, and integral control sub-loops. The PID control loop starts its functioning after taking input of the set-values [{q1, q2, q3], {qG}] at a particular time-instant. As illustrated in Figure 13, all four PID loops function in unison, but independently. The software routine of the control program has the provision for altering the numerical values of all these gains, viz. {Kp, Kd, Ki} for all the joints as and when felt necessary. The ab initio value of the proportional gain (Kp) is being set using the theoretically computed value of the natural frequency of vibration (in Hz.). We have used a nomograph for selecting the particular value of ‘Kp’ ~ wherein the basic nomograph was framed using experimental data from the strain gauges. The other two gains, viz. derivative (Kd1) and integral (Ki)are set by determining the fluctuations in the values of the natural frequencies of vibration over a pre-defined time period of operation of the FRS. Essentially, initial set-values of all three gains are arrived at by changing the mass at the FRS-gripper (payload)~ this mass is responsible for the degree of oscillation in the system, and alteration of that gets registered by the strain gauges. While ‘Kd’ is chosen via the monograph for the variation of the strain gauge values in the two consecutive time-instants, say ti and t i+1, the selection of the set-value for ‘Ki’is made through another nomograph for the arithmetic mean of the strain gauge values in the said two consecutive time-instants. Once the initial values of these three gains are set, the next rounds of alterations in the gains are governed by the custom-made program code. With the changes in gains, the overall Laplace Transform for the PID loop also gets altered for each FRS-joint. Likewise, the modulations can be effected for the PID sub-loop of the FRS-gripper as well. It is apparent that the overall PID loop will be uncertain to a certain extent because of the vibration characteristics of the FRS-links and hence some of the existing models nay not be the appropriate [47,48] as well as reinforcement learning (RL) in recent past [49].
The output of the PIP sub-loop is fed to the vibration (frequency) attenuation module (VAM), respectively for each FRS-joint as well as FRS-gripper. The functioning of this module is time-dependent and it computes the time-summation of all the frequency alterations for each FRS joint and FRS gripper. In other words, the module computes at every time-instant, ti, the summation of the change in vibration frequency in two successive preceding time-instants, say, ti-1 and ti-2. The program-counter for this module gets refreshed each time-instant and the updated value is added up to the PID-loop output value. The idea of this ‘addition’ is to make the PID-loop more robust so that the feedback loop gets fine-tuned more efficiently by taking into account the effect of vibration in real-time. Nonetheless, the software program routine of the controller is capable of ‘hiding’ this vibration attenuation module, which can be used to study the effect of the PID loop only on the controller performance as a theoretical research metric. The system will attain stability with the PID loop too, but, it will definitely be much advantageous to augment VAM with the PID so far as the attainment of stability of the FRS is concerned.
The final summation is passed into the servo (feedback) loop as ‘error’ values, viz. [{e1, e2, e3}, { eG}]. Amplification of these error values by means of non-unity amplifier gains has been invoked in the control system algorithm that is entrusted to provide better stability towards harnessing the in-situ vibration of the FRS. The non-unity amplifier gains are uniform for the three joints of the FRS (li), while it has a different value for the FRS-gripper (lg).
The culmination of the servo-control algorithm takes place after the feedback loop is set in real time. The controlled output values of the joint-angles of the FRS as well as rotation of the motor-shaft of the FRS-gripper are noted as system-tuple, viz. [{f1, f2, f3}, { fG}]. The step-wise modulation of the set-values of the joint-angles of FRS to the controlled values in real-time is fully indigenous and it draws attention toward effective real-time handshaking between PID and VAM sub-loops.
B. Development of the indigenous controller of the FRS: The controller of the prototype FRS, developed indigenously, has its foundation in the Faulhaber™-make Motion Controllers (MCBL and MCDC series), responsible for the actuation of its revolute joints. The proprietory motion controllers are used in the development of the ensemble controller of the FRS because of their compact ensemble and trouble-free mating with the servomotors of the same make. This decision has been found to yield rich dividends as vibration control in real-time needs much pruning of the controller architecture as well as software coding, out of which compatible tuple of servomotor- motion controller has definitely eased the troubleshooting. Figure 14 presents the general block diagram of the developed controller of the prototype FRS.
Functionally, the indigenously developed controller of the prototype FRS is constituted of four units, namely: [I] Power Supply Unit (PSU); [II] Joint Movement Module (JMM); [III] Sensor Processing Module (SPM) and [IV] Limit Switch Unit (LSU: having a set of 3 units, viz. LS1, LS2 and LS3). While PSU is an integral part of the entire controller, LSU is mainly related to JMM. Three limit switches of the LSU are located at the respective joint locations, i.e. those are affixed at different zones of the FRS (LS1 is being activated for joint 1 and so on). JMM consists of servomotor assemblies (motor, gearbox, and encoder integrated) for all three joints of the FRS. On the other hand, SPM takes care of strain gauges (for the joints) and flexi-force sensors (for the mini-gripper), with real-time calibration and settings. It is important to note that JMM and SPM are inter-correlated and both units are equally contributing towards smooth functioning of the FRS-controller in real-time. The SPM is constituted of two types of sensory elements, namely: a] semiconductor-type high-precision strain gauges (for the FRS-links) and b] flexi-force sensors (for the FRS-gripper). Both of these sensor-cells are very delicate to handle and crucial so far as instrumentation is concerned. Flexi-force sensors do possess a higher level of precision, improved repeatability, and linearity as compared to other commercially available varieties of force-sensing resistors. So far as the output of SPM is concerned, strain gauges are being instrumented through Wheatstone bridge circuitries, while flexi-force sensors have built-in bridge-balancing circuitry. Nonetheless, we need calibration of the sensor-cells before final instrumentation and it has been carried out through multiple trials off-line. The prototype FRS gets activated through 12V D.C. power source input. The PSU is made with two identical 12V D.C. supplies inside the housing. Either of these two power supplies can be used to charge a 70 Ampere- The Hour battery if needed.
The novelty of our work is in direct handshaking between JMM and SPU, which was not attempted earlier [50-53]. Although several control semantics using finite element-based dynamics [54-56] or erstwhile chronological modules of adaptive control [57-58] or payload-based non-linear control [59-66] do provide useful links for combating run-time oscillation dynamics of a multi-d.o.f. FRS, the aspects of experimental evaluation of such dynamics were hardly attempted.
The system controller is provided with an easy switch-over from electrical to battery-based activation of the FRS under indoor conditions, in case the situation demands so. Precaution should be adhered to for outdoor applications, as factors like heavy rainfall, direct sunlight, dust, excessive water slippage, or similar exposure to water can cause damage to the units of the controller box. The LSU of the prototype FRS takes care of unavoidable overrun of the joints in clockwise as well as counter-clockwise directions for protecting the servomotor of each link-joint sub-assembly. The LSU has been augmented with the FRS-controller quite effectively so that the individual limit switch gets triggered at the extreme ends of the links and mini-gripper. The control system program code has been syntaxed to give priority to the functioning of the limit switches. The program code inducts binary output of the limit switches and ensures complete stopping of the servomotor(s). All four motor controllers of the prototype FRS were interfaced with the serial RS232C port of the system computer for seamless data communication in an easy way. It may be noted that the basic logic of functioning of all Faulhaber™ motor controllers is the same despite different models of Faulhaber™ motors used in the hardware. The Faulhaber™-Motion Manager software has been instrumental in controlling the overall functioning of all four servomotors of the FRS and the motor for tripod movement. The indigenously developed control system program has good handshaking with Faulhaber™-Motion Manager software, as the later has user-selectable drop-down menus for the desired control parameter.
C. Experimentation with the prototype FRS and test results: The prototype FRS was critically examined for its performance in real-time through different sets of trials and tests. These tests are beyond the usual calibration of the sensors, which are aimed towards assessment of the real-time characteristics of the FRS. The two most significant as well as salient aspects of this real-time performance are a] evaluation of the ensemble strain in the FRS-links and FRS-gripper and b] determination of the natural frequency of vibration of the FRS. Real-time data from the strain gauges, mounted over the exterior of the FRS-links, symbolized the out-of-balance voltage of the respective Wheatstone bridge circuitries of the strain gauges. These voltage values were further deduced to evaluate the final data for strain in the FRS-member. In order to attain better accuracy of the experimental results, each strain gauge was put in the instrumentation as a single entity, and the corresponding Wheatstone bridge was made as a quarter-bridge. A total of 10 strain gauges were fixed on all three links of the FRS, out of which six were mounted on the first link (length: 800 mm.) two each on the second link (length: 400 mm.), and a third link (length: 200 mm.) respectively. These 10 strain gauges have separate quarter-bridge instrumentation that was augmented under SPM (refer Figure 14). Likewise, the mini-gripper of the FRS is provided with 2 nos. flexi-force sensors, having in-built Wheatstone bridge circuitry. The raw data output of these two flexi-force sensors in miilivolts was processed separately to get the strain values, using a calibration curve of said sensor. Tables 1,2 present the ensemble dynamic strain values of 10 nos. strain gauges and 2 nos. flexi-force sensors respectively, as obtained during various time-intervals under different trial-runs. Dynamic strain values were computed from the raw data of the strain gauges. These sensor units have been named S1, S2,……, and S12 in a sequential manner (starting from Link1 and ending with the mini-gripper). We have computed the average values of strain for a specific FRS-member also using these processed data on strain, e.g. {Av. e}1 is the average value of the strain for the 1st. link of the FRS that is computed as an average of numerical values of S1, S2,.., S6. Likewise, we can compute the average strain values foe 2nd. and 3rd. link of the FRS as well as FRS-gripper, which are nomenclated as {Av. e}2, {Av. e}3 and {Av. e}G respectively.
We should note a couple of paradigms in the trials, as presented above via Tables 1,2. The first and foremost aspect is related to the trials itself. All of these 12 trials have been time-synchronized, i.e. these trials have been undertaken chronologically. The raw data of the strain gauges have been generated through qualitative forcing at the tip of the distant link as well as at the gripper-end, executed manually. The forcing function is essentially touch type with a mild jerk during the later part of the trials. The computed values of the dynamic strain in FRS-links and FRS-gripper show mild variation in numerical values; but, in general, it was found to be high in the 1st. link. This sort of variability is usual in any self-trembling dynamic systems and our prototype FRS is no exception. The strain values at the FRS-gripper are slightly more in comparison to that at the 3rd. link of the FRS. This increment of the strain at the FRS-gripper can be attributed to the local stress and strain thereof, due to its tiny linkage structure and overhung. Apart from observing the numerical values of the strain in Tables 1,2, we need to dwell upon the query on an optimal number of the strain gauges (for FRS-links) and flexi-force sensors (for FRS-gripper) as well as the layout of those. From the computed data of Tables 1,2, it can be inferred that there are minor variations in the strain values across the intra-link strain gauges, i.e. those fitted on the same link of the FRS. Nonetheless, there is some variation in strain values between the inter-link strain gauges, i.e. those fitted on different links of the FRS. In other words, strain gauges on the FRS-1st link vis-à-vis that on the FRS-2nd or the FRS-3rd link show variations. Flexi-force sensors do have slight variations in readings, which are reflected in the computed strain values. We will now examine the computed data on the natural frequency of vibration (in Hz.), as obtained through several trials on the prototype FRS. Although various links of the FRS as well as the FRS-gripper will have marginally different values of the natural frequencies of vibration under free-form undamped motion, for the sake of ensemble analysis we will consider here the vibrational frequency at the distal part of the FRS, viz. at the tip of the third link of the FRS and the gripper-end. It is true that under the natural condition of joint rotations of the FRS, there will be built-in oscillations in all three links of the FRS as well as the FRS-gripper. These oscillations and ensemble trembling of the FRS-links are not coupled all the time and due to this, we get different deflection hues for the links. There are various pathways to study the patterns of deflection hues and subsequent oscillations of the FRS-links, which get translated to robust analytical models for evaluating vibration-related parameters of the FRS under real-time dynamics. In its simplest form, we will consider here the undamped free vibration of the FRS-links, without any external forcing. This free vibration model has been selected in order to study the natural pattern of deflection/trembling of the FRS due to its own inherent dynamics, namely, the rotation of its joints via the servomotor system. This natural oscillation paradigm of the FRS is also supplemented with two facets, viz. a] no external forcing on any of the FRS-member in any form (i.e. condition of ‘forced vibration’ is excluded) and b] no viscous damping from the exterior of the FRS ( i.e. condition of ‘viscous damping’ is excluded). Our study, experimental investigation, and finally, the numerical assessment of the natural frequency of vibration of the FRS is based on this basic paradigm of undamped free natural vibration. It is customary to adhere to the traditional ‘spring model’ to designate free vibration of the FRS-link. However, the criticalities in vibration signature will emerge due to several natural causes, thereby producing varying amplitude-frequency of the induced vibrations in different links of the FRS. This is a very obvious process and it is system-generated. The challenge lies in the accurate and effective modeling of this varying vibration using the spring model. The physical parameter of a spring that goes instrumental in characterizing the performance of the spring, i.e. its elongation and subsequently natural path-way of oscillation in the vertical plane, is nothing but its stiffness matrix. In the uni-axial deformation model of the spring, this stiffness matrix is analogous to the spring constant; ‘K, having dimension: MT-2 (force per unit length). As all other parameters of the FRS-links are essentially material-specific or design-specific, it is the value of ‘K’ that controls the numerical value of the natural frequency of vibration. However, the value of ‘K’ is the effective value, which is to be obtained through various combinations of placement of the spring in the model. Further, the value of ‘K’ may not be equal in all such combinations; and, we may use non-identical springs with different values of the spring constant. These are all modeling paradigms that need to be ascertained to capture the characteristics of the free undamped vibration of the FRS-members. Figure 15 shows the schematic disposition of this undamped free natural vibration scheme of any FRS-link. It is noteworthy to highlight various possible combinations of spring systems, as extended manifestations of series and parallel layout (refer Figure 15: # I to X). Standard formulae of the series-parallel combinations will be used to compute the ensemble spring constant, considering equal values of ‘K’ in all these 10 layouts. Numerical treatment will remain the same in case of multiple different springs with unequal values of ‘K’, say K1, K2, K3,…etc. are used in the model.
We know that numerically, the natural frequency of vibration is a function of the ‘K’ and ‘mass’ of the vibrating member, as per the postulation of natural vibration. As there is no alteration in the ‘mass’ (‘m’) of the vibrating member, the sole dependency of the natural frequency of vibration (fn) will be on the ‘equivalent spring constant’ (Keq) of the FRS-link system. This proposition does justify the lemma of Figure 15 with its 10 different poses of spring layout. This direct proportional relationship between ‘fn‘ and ‘Keq’ is the crux of the engineering aspect of the study of the undamped free vibration of FRS-link(s) and FRS-gripper. Thus, it essentially boils down to the near-optimal numerical evaluation of ‘Keq.’ using the known parameters of the FRS.
Researchers have tried out a few methods for the control of this in-situ vibration of FRS, such as i] fuzzy-based model [67-69], ii] state linearization [70], iii] end-effector trajectory control [71], iv] feedforward/feedback control [72-74], and v] payload-induced dynamics [75]. Unlike these methodologies, we have incorporated various combinations of springs to symbolize the ‘extent’ of oscillation.
It is interesting to observe the dispositions of the spring-elements in the layout of Figure 15 and to be specific, the gradual variation of complexity of the layouts. By default, the first layout is the simplest with only one spring-element, having spring-constant ‘K’. The next two schemata, viz. layout #2 and #3 represent series and parallel combinations of spring elements in simplest form. Layouts # 4 and 5 involve three spring-elements each, disposed of in two geometrical variants. Two extended versions of layout #4 are depicted in the next two schemata, namely, layouts # 6 and 7. The complexity of the computation of ‘Keq.’ begins from layout # 6 and continues thereon. We introduce new sub-schemata of the ‘star-delta connection’ of spring-elements in the next three layouts, viz. layouts # 8, 9, and 10. While layout # 8 shows the basic star-delta type spring-elements, complexity gets infused in layout # 9 with additional spring-elements, adjoining the basic star-delta. The last layout is a boolean combination of layouts # 7 and 8 and it is, by virtue, the representative of all such possible boolean combinations of layouts of the spring elements in a FRS-link.
Numerical evaluation of the natural frequency of vibration is traditionally theory-based and for a specific material and known mass of FRS-link, it is directly proportional to the spring constant or ‘Keq.’, depending upon the layout schemata. Interestingly, ‘K’ is also dependent on the geometry of the FRS-link as well as its material. In a way, we get a tuple to evaluate the natural frequency of vibration, fn, of the FRS-link system, as shown below:
Where, m: mass of the FRS-link; F: in-built force acting on the link to cause vibration; A: cross-sectional area of the link; L: length of the link; Y: Young’s modulus of the material of the link; d: deflection of the link (in the direction of in-built forcing function).
Thus, as per theory, the working formula for the numerical evaluation of ‘fn’ becomes (using eqns. 12 and 13),
Where, D: diameter of the FRS-link and r: density of the material of the FRS-link. The rest of the symbols have been named earlier in eqns. 12 and 13. As an off-shoot to the evaluation of fn, we can deduce the working formula for the ‘force of vibration (‘F’), which is essentially a theoretical and imaginary attribute. Since we are not considering the situation of forced vibration here we will only look at the expression for ‘F’ as a direct function of the average strain obtained in the FRS-link, as shown below:
Now, as per experimental observation, let us take a look at the average strain values of Table 1. We can compute the ‘force of vibration’ for a specific FRS link at various time-instants with different combinations of joint angles for the ensemble motion of the link using eqn. 15. Taking into consideration the identical geometry of all FRS-links, namely the same cross-section and material, we can estimate ‘Force of Vibration’ (FOV) values for all three FRS-links separately. Now, the proposition will take an interesting finding if we need to estimate the ‘Average Force of Vibration’ (AFOV) for the FRS in totality. The nucleus of the model is rooted in the phenomena of twisting of the FRS-joints due to this natural trembling of the system and the FOVs in particular. The joint twist is an inherent phenomenon of the FRS and it can be mathematically expounded with the help of ‘moments of the force’, computed numerically with respect to the quadrature plane. The estimation of AFOV can be made by imagining an equivalent FRS by adopting the concept of ‘Flexible Uni – Equivalent Link ‘ (FUEL). In a nutshell, FUEL will have one link only, which will be capable of generating the same ‘moment of force’, as obtainable from the 3-link FRS, or, in general, FUEL will be the ‘analytical clone’ to an N-link serial-chain FRS. Hence, AFOV will be estimated using the simple ‘Moment Balance’ principle for FUEL, without taking into account any additional effect such as torque of the revolute joints or the viscous force at the link-joint interfaces. We also assume a homogenous distribution of mass of the links over their lengths that correspond to the locations of the centres of gravity for the links at the respective midpoints. All these parlances are important to bring out a basic estimate of AFOV and the same can be utilized for ascertaining the extent of trembling or drooping of the multi-link FRS. It is crucial to adopt a near-optimal methodology for evaluating AFOV using simple mechanics. Taking a re-look at the disposition of our FRS (refer to Figures 3 and 8), we can now postulate the analytical model of FUEL using ‘Moment-balance Lemma’ as:
Where, {L1, L2, L3}: the length of the three consecutive links of the FRS; {F1T, F2T, F3T}: tare weight of the links in succession; FGT: tare weight of the gripper; FAV: Average Force of Vibration (AFOV) of the ensemble FRS (including gripper). It is to be noted here that we have considered only the force balance lemma of the ‘Free-Body FRS’ with no external impulse or forcing.
The right-hand side expression of eqn. 16 is essentially the paradigm of FUEL, in which we have considered the full planar stretch of the manipulator having a total length of (∑Lj), ∀j = 1,2,3. Equation 16 brings out that for a prototype FRS with fixed dimensions, AFOV is a stable value. Numerically, the value of AFOV so obtained signifies the extent of trembling of the FRS due to its natural weight only (without any external forcing). Nonetheless, as a maiden step of evaluation of AFOV in real-time, the other two moment-components, namely: a] viscous force at the link-joint interface and b] in-situ torque at the joint (generated due to twist, turn, and angular displacement) have been omitted in the formulation of eqn. 16.
The Flexible Uni-Equivalent Link deals with two kinds of forces, namely: a] tare weight, ‘FT’, and b] force due to vibration, ‘FV’. While FT will act vertically downwards through the centre of gravity of FUEL, FV can act through a co-planar point, other than the centre of gravity. This is true for all links of the FRS as well if we take their free-body-diagrams. In fact, the ‘line of action’ of FV for every FRS-link and /or FUEL is through the line/region of maximum strain. While FV can be evaluated numerically for each link of the FRS based on the average strain of that link, the average force of vibration, AFOV needs to be estimated through the moment-balance equation only. As a matter of fact, the numerical value of ‘FAV’ (refer eqn. 16) is a coupled form of the tare weight of FUEL and the force due to the vibration of FUEL. However, there is no experimental procedure possible to identify and evaluate these two components separately.
Considering the material of construction of the FRS-links to be Carbon Fibre Reinforced Plastic (CFRP), we get the average value of ‘Y’ as 181x109 N/m2. Taking into account that the as-fabricated diameter of the FRS-links is 10 mm., we can calculate the numerical estimates of the ‘force of (due to) vibration’‘FV’ by using the model of eqn. 15. As evident, the estimate of ‘FV’ is directly proportional to the average strain values of the respective links. It may be noted that average strain is an imaginary entity so far as its ‘point of execution’ is concerned. In the case of the present prototype, ‘FV’ is numerically equal to (1422.1428x 104) times the average value of the strain obtained experimentally. These data on ‘Force of Vibration’ for the FRS-links, namely, ‘F1V’, ‘F2V’, and ‘F3V’ as well as ‘Average F’(experimentally) are presented in Table 3 below. The computed data of Table 3 shows that the maximum force of vibration occurs at the first link of the FRS, indicating the largest trembling at the first link. The force of vibration gradually smoothens off in the subsequent links.
Now, in order to compute the numerical value of AFOV, vide eqn. 16 we need to evaluate the tare weights of the FRS-links and FRS-gripper. Considering the average value of the density of CFRP (in rod form) as 1800 kg/m3, we can evaluate the weights of the FRS-link having a circular cross-section with an identical diameter of 10 mm. For example, the tare weight of the first link of the FRS (F1T) will be equal to 0.1131428 kgf [ (1800). (0.8) . p . (0.01)2/4 ]. Likewise, the numerical values for F2T and F3T will be equal to 0.056571 kgf and 0.0282857 kgf respectively. The calculations have been arrived at by taking the lengths of the FRS links, viz. L1, L2, and L3 as 0.8m, 0.4 m and 0.2 m respectively. The tare weight of the mini-gripper has been measured separately as lumpsum mass and it was found to be 100 g. Accordingly, FGT has been recorded as 0.1 kgf. Hence, the numerical value of the AFOV can be evaluated as 0.397999 kgf or 3.90437 N (using eqn. 16; acceleration due to gravity: 9.81 m/sec2). As per the conceptual lemma of ‘FUEL’, AFOV is acting through the centriod of FUEL, which is commensurate to the postulation of eqn. 16. Interestingly, if we are focused on the estimation of the ‘average force of vibration’ at the tip of the gripper-point of FUEL, then the value of AFOV will be 0.198999 kgf or 1.95218 N. We have used the total length of FUEL as 1.4 m in this case. Further, it is to be noted here that ‘FiT’ and ‘FiV’, ∀i = 1,2,3 will not act simultaneously as ‘FiV’ is imaginary.
Let us now focus on the determination of the natural frequency of vibration of the FRS, which will start with the evaluation of the same from a theoretical perspective, separately for all three links of the FRS. We have used the working formula of eqn. 14 for this, with the incorporation of the average numerical values of ‘Y’ and ‘r’ as 181x109 Nm-2 and 1800 kgm-3. Accordingly, the theoretical value of the natural frequency of vibration of the first link of FRS will be (1595.32216 / 0.8) or 1994.15 Hz. Likewise, the natural frequency of vibration of the second link of FRS will be (1595.32216 /0.4) or 3988.31 Hz. Finally, the value of the natural frequency of vibration for the third link of FRS becomes (1595.32216 /0.2) or7976.61 Hz. It is to be noted that we can even estimate the natural frequency of vibration of ‘FUEL’ by the same formula. In our case, the length of FUEL is 1.4 m, and accordingly, the numerical value of the natural frequency of vibration of FUEL will be: (1595.32216 / 1.4) or 1139.51 Hz.
Experimental determination of the natural frequency of vibration of the FRS-link(s) and/or FRS-gripper is crucial. We need to evaluate it with the help of mere strain gauge data. There is no other way out and besides strain gauge data (of dynamic strain), we can’t even arrange any other instrumentation in real-time for such an assessment. This is the greatest irony of a FRS and we have to deal with it so far as the estimation of in-situ vibration / natural frequency is concerned. The experimental runs are essentially made with the help of activation of the joint servomotors of the FRS in a selected pattern. In that sense, the experimental runs are representative of the pseudo-forced vibration of the FRS. Although there is no external forcing function acting on the FRS members, the vibration is being forced into the system by means of the rotational motion of the joint motor(s). Since the prototype FRS is a direct-drive system (refer to schematics of Figures 2 and 3 and actual photographs of Figures 8 and 9), we can operate the FRS by rotating any one joint or augmenting control commands for different combinations of joint angles. In either of the cases, the cumulative run-time torque of the motor shaft will be responsible for the rotation of the joint(s), and that will finally culminate in the pseudo-forced vibration of the FRS members. In other words, the force of vibration, so generated, can be evaluated from the motor-torque value(s), as obtained from the Graphical User Interface. So, we can measure two sets of data in real time, namely the strain gauge data and motor-torque data, in every test run of the FRS. While real-time data from strain gauges will be instrumental in deducing the ensemble deflection of the FRS member, the motor-torque data will be used to evaluate the effective forcing (AFOV) at a specific FRS member. As per the layout scheme of the prototype FRS, the motor-torque vector and AFOV vector are co-planar and are separated by a linear distance equal to the length(s) of the FRS-member(s). It is to be noted here that this ‘linear distance of separation’ can be cumulative, i.e. addition of several link lengths if we need to estimate AFOV at a distal link of FRS. The formulation can be made generic as well for ‘N’-link FRS.
To begin with, we will investigate the phenomena of pseudo-forced vibration of the FRS-member(s) under the excitation created by only one servomotor of the FRS joint. Here we assume that all joints of the FRS are identical in all respects hardware-wise and accordingly, all joint-servomotor systems are equally likely. We also pre-condition that during the activation of the specific joint-servomotor, the rest of the joint motors are not actuated and thus, those remain in their then state of angular postures. With this proposition, the computational formula for the natural frequency of vibration of the Nth. member of a ‘N’-link serial-chain FRS under this state of pseudo-forced vibration can be deduced from eqns. 12 and 13, as described below:
Where, fnN: natural frequency of vibration of the Nth. member (link) of the N-link FRS; Keq.N: Equivalent spring constant for the Nth. member of the FRS; mN: Mass of the Nth. member of the FRS; Flinkv: Pesudo Force of Vibration at the Nth. member of the FRS; dN: Deflection occurred at the Nth. member of the FRS; eAv.N: Average strain obtained at the Nth. member of the FRS; LN: Length of the Nth. link/member of the FRS; r : Density of the material of fabrication of the FRS; AN: Cross-sectional area of the Nth. member of the FRS; tmotor(k): Run-time torque of the kth. servo-motor of the FRS (∀k = 1,2,…N).
It may be observed that eqn. 17 is the generic format of evaluation of the natural frequency of vibration of the multi-jointed FRS member that can be the link of the FRS or its gripper. As per the lemma behind the formulation of eqn. 17, we are considering the situations wherein only one servomotor is being activated to create the pseudo-forced vibration scenario Hence, the source of the vibration, so generated, is the excitation of the system due to the activation of any one of the revolute joints of the FRS. The very servomotor is responsible for the actuation of the corresponding revolute joint of the FRS. All the servomotors of the FRS are pre-programmed through the control system of the FRS and the run-time torque of the motor-shaft can be obtained from the control system programming as well as its Graphical User Interface (GUI).. Nonetheless, the choice of the particular servomotor that is to be activated along with its extent of activation (joint movement in degrees) is user-selectable. During this programmed activation, the rest of the servomotors are kept under non-activation mode. It is to be noted here that eqn 17 is valid if we do not consider any retarding torque due to the joint rotation of the preceding link(s). The formulation will alter under real-life situations wherein the pseudo-forced vibration takes into account of impedance of the joint that is being actuated by the servomotor. This joint impedance results in a retardation torque and its numerical extent gets defined by a factor, named, ‘joint retardation coefficient’. The effect of the joint retardation will be on the preceding link(s) of the FRS, with respect to the joint-servomotor that is being activated. The revised formula for the evaluation of the natural frequency of vibration of the FRS member under this real-life situation of joint retardation is texted below:
Where, fn*N: real-life natural frequency of vibration of the Nth. member (link) of the N-link FRS under joint-retadation effect; eAv.N: Average strain obtained at the Nth. member of the FRS; LN: Length of the Nth. link/member of the FRS; r : Density of the material of fabrication of the FRS; AN: Cross-sectional area of the Nth. member of the FRS; tmotor(k): Run-time torque of the kth. servo-motor of the FRS (∀k = 1,2,…N); l: Joint Retadation Coefficient (JRC), 0< l≤0.1.
The syntax of the natural frequency of vibration under a pseudo-forced vibration situation gets computationally complex if two or more servomotors are in simultaneous activation. In such cases, the effective force of vibration on a FRS member will be multi-sourced and evaluation has to be made accordingly. We will deal with that formulation in the next part of the paper.
The other crucial aspect of the experimental evaluation of the natural frequency of FRS-member(s) is a selection of the ‘trial ensemble’. We need to freeze out the total number of trial runs that are to be conducted for a particular FRS member and decide on the composition of those trial runs. For example, if we are going to evaluate the natural frequency of vibration of the third link of the FRS, then we have to decide whether all trials will be conducted by activating one servomotor only (keeping the other two servomotor at zero motion) or not. If we decide on doing the trials under the joint motion of one specific servomotor only, then we need to alter the amount of joint movement (angular motion in degrees) through the FRS controller. This method is, by and large, simple and convenient so far as the modulation of the control system logic of the FRS is concerned. Nonetheless, we still have the choice of selecting the servomotor to be activated, e.g. FRS-3rd. link can be excited either by the activation of the first joint-motor, the second, or even the third. Obviously, we will get slightly different sets of natural frequencies in those 3 verticals, viz. case I: activation by joint-motor#1; case II: activation by joint-motor#2, and case III: activation by joint-motor#3.
Nonetheless, real-time excitation of the FRS-3rd. link can be ascertained with simultaneous activation of all three joint-motors too. As a matter of fact, for a 3-link 3-degree-of-freedom serial-chain FRS, there will be 23 or 8 different feasible combinations of joint angles that are equally likely to cause excitation to the FRS member (s). In general, we can have a total of 2N different combinations of joint angles possible for the pseudo-forced vibration of an N-link serial-chain FRS.
The readings so obtained (run-time motor torque and average strain) can be compared, followed by a study on the computed values of the natural frequency of vibration of that very FRS member. The said comparison of the numerical values of the natural frequency of vibration is also important as we can get the values through various combinations of joint angles. Since pseudo-forced vibration is possible in multiple ways, we need to specify the method used to obtain the said values of ‘fn’ in the data table.
The other important factor in the experiment is the number of trial runs and inter-trial comparison of data. For example, if we decide to undertake 10 trials under a specific methodology of excitation of the FRS-member(s), then the intra-trial comparison can be made within that envelope. Likewise, we can get another set of 10 data when we invoke a different methodology of excitation. It is true that finally, we can evolve a global average of the said ‘fn’ for the specific FRS member.
In our case study, we will first register experimental data with respect to the activation of the first joint-servomotor of the FRS only and we will investigate the effect of such excitation on the third link of the FRS as well as the FRS-gripper. In other words, the first joint-motor will be activated by various combinations of current and torque so as to produce variations in the joint angle of the first revolute joint of the FRS. As explained earlier, the other two joint-motors will be in non-activation mode and those will not be considered for any effective torque calculation. We are excluding the details of the joint-angle sets of the first joint of the FRS, so generated. In order to perform the experiments in real-time, we have adhered to the design data sheet of the servomotor and accordingly, we have selected the combinations of current and torque in such a way that those do not exceed the rated value of the torque at a specific tine-instant. Table 4 presents the experimental data against 10 trial runs and also the computed values of the natural frequencies of pseudo-forced vibration for the distal /third link of the FRS, while activated by the first joint-servomotor. The results have been arrived at by using the formula of eqn. 17. All values of the run-time torque of the first joint motor have been selected based on the suitability of the FRS controller to tune the run-time current, not overshooting by more than 0.4% of the rated torque value.
It is worth noting that the values of the average strain of the FRS-third link are deduced in real-time, based on the in-situ excitation as well as the trembling/vibration of the distal link. These values are largely in the same order as that of Table 3, numerically. It is obvious that finer results of the natural frequency of vibration can be obtained if we augment more strain gauges over the surface of the FRS-third link. But, on the flip side, instrumentation of a larger number of strain gauges is equally challenging technologically.
Let us now focus on the experimental evaluation of the natural frequency of pseudo-forced vibration of the FRS-gripper under the excitation via the first joint motor. As before, results will be identical for both cases, viz. ‘without JRC’ and ‘with JRC’. However, the length of the effective ‘link’ that will be affected by this vibration will be (Total horizontal span of FRS) + (Breadth of the gripper in the frontal plane). Considering the breadth of the FRS-gripper as 20 mm., the effective ‘link-length’ undergoing vibration will be: 1400 mm. +20 mm. = 1.42 m. The effective ‘cross-sectional area’ of the FRS-gripper will be the planar area undergoing vibration, namely the rectangular area, constituted by the length and width of the gripper. Hence, the cross-sectional area of the FRS-gripper that will be useful for the computation of ‘fn’ will be 50 mm x 15 m. = 75x10-5 m2. However, we have to take note that this cross-sectional area is a kind of maximum possible area that can be exposed to excitation. In fact, it is difficult to numerically compute the ‘actual’ cross-sectional area of the FRS-gripper that is facing excitation, because of its intricate geometry and design features. The density of the gross material of fabrication of the FRS-gripper (teflon) will be 2200 kg/m3. Table 5 presents the experimental data against 10 trial runs and also the computed values of the natural frequencies of pseudo-forced vibration for the mini-gripper of the FRS, while activated by the first joint-servomotor. As before, the results have been arrived at by using the formula of eqn. 17. As explained, the values that we obtain for the natural frequency of vibration will be a kind of ‘upper bound’ values and those will indicate a reasonably safe threshold for the design of the control system of the FRS. If we analyze the background computation of the cross-sectional area for Tables 4,5, we will get a clear understanding that the cross-sectional area of the FRS-gripper is nearly 10 times larger than that of the FRS-link. Quite obviously, the computed values of the natural frequency of pseudo-forced vibration for the FRS-gripper will be much higher than that of FRS-3rd. link.
We will shift our attention now to the pseudo-forced vibration of the distal link again, but, this time, under the excitation of the second joint-motor. However, we will take into account the effect of the joint retardation coefficient by assuming a moderate value of ‘l’ as 0.05. In other words, we will report the computed values of the natural frequency of vibration of the FRS-third link for both cases, viz.:a] without taking into account the joint retardation and b] with due consideration of the joint retardation effect. We will report the experimentally determined values of the natural frequencies in both cases, vide formulae of eqns. 17 and 18. Table 6 presents the experimental data against 10 trial runs and also the computed values of ‘fn’ of pseudo-forced vibration for the distal /third link of the FRS, while activated by the second joint-servomotor. We have observed the increment of the numerical value of ‘fn’ between case [a] and case [b], referred to above.
Finally, we will report the experimentally determined values of the natural frequencies of pseudo-forced vibration for the distal /third link of the FRS, while activated by the third joint-servomotor. Table 7 presents the data for 10 trial runs and the computed values of ‘fn’, under two cases, namely, ‘without JRC’ and ‘with JRC’.
If we observe the numerical values of the natural frequency of vibration of the FRS-3rd. link, there is a factor of multiplication of sqrt(5.050505) while the excitation is made by the first joint-motor (without JRC). Likewise, the factor of multiplication is sqrt(11.784511) for the excitation done with the actuation of the second joint-motor (without JRC). Finally, during the excitation made by the activation of the third joint-motor (without JRC), the factor of multiplication becomes sqrt(35.353535).
Conclusion
We have delineated the technicalities of the indigenous hardware of a prototype serial-chain three-link flexible robotic system in this paper, backed up by experimental results. This detailed research on flexible robots will be instrumental in creating novel designs for similar FRS with sensory instrumentation. Besides hardware details, a new model for the in-situ vibration signature of a multi-link flexible robotic system using spring-sub-system and strain gauges is also reported. The system dynamics of multi-link FRS are quite different from that of single-link flexible robots due to the coupling effects of joints and its drive-train, along with the run-time program. Scientifically ascertained locations of augmentation of strain gauges on the FRS-links play a crucial role too in the overall target of achieving smoother control of the system dynamics, through the evaluation of natural frequency of vibration of the FRS-members in real-time. The present research builds up an optimal foundation for analyzing the inherent vibration of flexible robots and their performance in gripping small payloads in real time.
The author acknowledges the help rendered by Shri Uday Phalnikar, Ex-Prolific Systems and Technologies Pvt. Ltd., Thane, India in assisting the hand-made sub-assemblies of the links and gripper of the prototype FRS. The technical assistance provided by the engineers of M/s Devendra Fabricators, Nashik, Maharashtra, India is duly acknowledged on the fabrication of the prototype flexible robotic system.
- Benosman M, Vey G. Control of Flexible Manipulators: A Survey. Robotica. 2004; 22: 533-545.
- Fraser AR, Daniel RW. Perturbation Techniques for Flexible Manipulators. Norwell, MA, Kluwer, 1991.
- Luo ZH. Direct Strain Feedback Control of a Flexible Robot Arm: New Theoretical and Experimental Results. IEEE Transactions on Automatic Control. 1993; 38: 1610-1622.
- Chen W. Dynamic Modeling of Multi-link Flexible Robotic Manipulators. Computers and Structures. 2001; 79: 183-195.
- Feliu V, Somolinos JA, Garcia A. Inverse Dynamics based Control System for a Three Degrees-of-freedom Flexible Arms. IEEE Transactions on Robotics and Automation. 2003; 19: 1007-1014.
- Feliu V, Ramos F. Strain Gauge based Control of Single-Link Flexible Very Light Weight Robots Robust to Payload Changes. Mechatronics. 2005; 15: 547-571.
- Subudhi B, Morris AS. Dynamic Modeling, Simulation and Control of a Manipulator with Flexible Links and Joints, Robotics and Autonomous Systems. 2002; 41: 257-270.
- Moudgal VG, Kwong WA, Passino KM, Yurkovich S. Fuzzy Learning Control for a Flexible-link Robot. IEEE Transactions on Fuzzy Systems. 1995; 3: 199-210.
- Singer NC, Seering WC. Preshaping Command Inputs to Reduce System Vibration. Journal of Dynamic Systems, Measurement and Control- Transactions of the ASME. 1990; 112: 76-82.
- Chen YP, Hsu HT. Regulation and Vibration Control of an FEM-based Single-link Flexible Arm using Sliding-mode Theory. Journal of Vibration Control. 2001; 7: 741-752.
- Tjahyadi H, Sammut K. Multi-mode Vibration Control of a Flexible Cantilever Beam using Adaptive Resonant Control. Smart Materials and Structures. 2006; 15: 270-278.
- Trapero-Arenas JR, Mboup M, Pereira-Gonalez E, Feliu V. Online Frequency and Damping Estimation in a Single-Link Flexible Manipulator based on Algebraic Identification. Proceedings of the 16th. Mediterranean Conference on Control and Automation (IEEE), Franco, 2008; 338-343.
- Pereirea E, Aphale SS, Feliu V, Moheimani SOR. Integral Resonant Control for Vibration Damping and Precise Tip-positioning of a Single-link Flexible Manipulator. IEEE/ ASME Transactions on Mechatronics. 2011; 16: 232-240.
- Zhang J, Tian Y, Zhang M. Dynamic Model and Simulation of Flexible Manipulator based on Spring and Rigid Bodies”, Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (‘ROBIO-2014’). 2014; 2460-2464.
- Feliu J, Feliu V, Cerrada C. Load Adaptive Control of Single-link Flexible Arms Based on a New Modeling Technique. IEEE Transactions of Robotics and Automation. 1999; 15; 793-804.
- Yang TC, Yang JCS, Kudva P. Load Adaptive Control of a Single-link Flexible Manipulator. IEEE Transactions on Systems Man and Cybernatics. 1992; 22: 85-91.
- Canon RH, Schmitz E. Initial Experiments on the End-point Control of a Flexible Robot. The International Journal of Robotics Research. 1984; 3: 62-75.
- Kotnick T, Yurkovich S, Ozguner U. Acceleration Feedback Control for a Flexible Manipulator Arm. Journal of Robotic Systems. 1998; 5: 181-196.
- De Luca A, Lucibello P, Ulivi G. Inversion Techniques of Trajectory Control of Flexible Robot-arms. Journal of Robotic Systems. 1989; 6: 325-344.
- Debanik R. Control of Inherent Vibration of Flexible Robotic Systems and Associated Dynamics. Invited Paper: Proceedings of the 8th. National Conference on Wave Mechanics and Vibrations (“WMVC-2018”), Rourkela, India, Nov. 2018; Springer Book, Lecture Notes in Mechanical Engineering. pp 201-222, ISBN: 978-981-15-0286; ISBN 978-981-15-0287-3 (eBook).
- Warude P, Patel M, Pandit P, Patil V, Pawar H, Nate C, Gajlekar S, Atpadkar V, Roy D. On the Design and Vibration Analysis of a Three-Link Flexible Robot Interfaced with a Mini-Gripper. Proceedings of the 8th. National Conference on Wave Mechanics and Vibrations (“WMVC-2018”), Rourkela, India, Nov. 2018; Springer Book. Lecture Notes in Mechanical Engineering. 29-46, ISBN: 978-981-15-0286- https://doi.org/10.1007/978-981-15-0287-3.
- Rauniyar A, Pandit P, Atpadkar V, Roy D. Design Model for the Drive and Actuator of the Test Set-up of a Novel Flexible Robotic System”, Proceedings of the 2018 IEEE International Conference on Computational Intelligence and Computing Research. (“IEEE ICCIC 2018”). Madurai, India, Dec. 13-15, 2018; 15-21.
- Debanik R. Towards the Control of Inherent Vibration of Flexible Robotic Systems and Associated Dynamics: New Proposition and Model”, International Journal of Robotics Research, Applications, and Automation. 2019; 1: 6-17. DOI: 10.18689/ijra-1000103.
- Tang L, Gouttefarde M, Sun H, Yin L, Zhou C. Dynamic Modelling and Vibration Suppression of a Single-link Flexible Manipulator with Two Cables. Mechanism and Machine Theory. 162: 104347; DOI: https://doi.org/10.1016/j.mechmachtheory.2021.104347.
- Hu FL. Ulsoy AG. Dynamic Modeling of Constrained Flexible Robot Arms for Controller Design. Journal of Dynamic Systems, Measurement, and Control—Transactions of the ASME. 1994; 114: 56–65. DOI: 10.1115/1.2900681.
- Neusser Z, Nečas M, Valášek M. Control of Flexible Robot by Harmonic Functions. Applied Sciences. 2022; 12: 3604; DOI: https://doi.org/10.3390/app12073604.
- Simo JC, Vu-Quoc L. The Role of Non-linear Theories in Transient Dynamic Analysis of Flexible Structures. Journal of Sound and Vibration. 1987; 119: 487–508. DOI: 10.1016/0022-460x(87)90410-x
- Gaultier PE, Cleghorn WL.A Spatially Translating and Rotating Beam Finite Element for Modeling Flexible Manipulators. Mechanism and Machine Theory. 1992; 27: 415–433. DOI: 10.1016/0094-114x(92)90033-e
- Li CJ, Sankar TS. Systematic Methods for Efficient Modeling and Dynamics Computation of Flexible RobotManipulators. IEEE Transactions on Systems, Man, and Cybernetics. 1993; 23: 77–95. DOI: 10.1109/21.214769
- Ata A, Fares WF, Sa’adeh MY. Dynamic Analysis of a Two-link Flexible Manipulator Subject to Different Sets of Conditions. Procedia Engineering. 2012; 41: 1253–1260. DOI: 10.1016/j.proeng.2012.07.308
- Theodore RJ, Ghosal A. Modeling of Flexible-link Manipulators with Prismatic Joints. IEEE Transactions on Systems, Man and Cybernetics Part B (Cybernetics). 1997; 27: 296–305. DOI: 10.1109/3477.558822
- Theodore RJ, Ghosal A. Robust Control of Multi-link Flexible Manipulators. Mechanism and Machine Theory. 38: 2003; 367–377. DOI: 10.1016/s0094-114x(02)00125-8
- Debanik R. Vibration of Flexible Robots: Dynamics and Novel Synthesis of Unbounded Trajectories. Annals of Robotics and Automation. 7: 001-018; DOI: https://dx.doi.org/10.17352/ara.000016.
- Rao P, Roy D, Chakraverty S. Vibration Analysis of Single-Link Flexible Manipulator in an Uncertain Environment. Journal of Vibration Engineering and Technologies. 2023; 1-18; https://doi.org/10.1007/s42417-023-01007-2.
- Wei D, Gao T, Mo X, Xi R, Zhou C. Flexible Bio-tensegrity Manipulator with Multi-degree of Freedom and Variable Structure. Chinese Journal of Mechanical Engineering. 2020; 33. DOI: https://doi.org/10.1186/s10033-019-0426-7.
- Yip MC, Camarillo DB. Model-less Feedback Control of Continuum Manipulators in Constrained Environments. IEEE Transactions on Robotics. 2014; 30: 880-889.
- Liu Y, Ge Z, Yang Sk, Walker ID, Ju Z. Elephant’s Trunk Robot: An Extremely Versatile Under-actuated Continuum Robot Driven by a Single Motor. Journal of Mechanisms and Robotics. 2019; 11: 051008; DOI: 10.1115/1.4043923.
- Calisti M, Picardi G, Laschi C. Fundamentals of Soft Robot Locomotion. Journal of The Royal Society Interface. 2017; 14: 20170101. DOI: https://doi.org/10.1098/rsif.2017.0101.
- Shiva A, Stilli A, Noh Y, Faragasso A, Falco ID, Gerboni G, Cianchetti M, Menciassi A, Althoefer K, Wurdemann H. Tendon-based Stiffening for a Pneumatically Actuated Soft Manipulator. IEEE Robotics and Automation Letters. 2016; 632-637; DOI: 10.1109/LRA.2016.2523120.
- Rus D, Tolley MT. Design, Fabrication, and Control of Soft Robots. Nature. 2015; 521: 467-475.
- Chalvet V, Braun DJ. Criterion for the Design of Low-power Variable Stiffness Mechanisms. IEEE Transactions on Robotics. 2017; 33; 1002-1010.
- Fardanesh B, Rastegar J. A New Model-based Tracking Controller for Robot Manipulators using the Trajectory Pattern Inverse Dynamics. Proceedings of the IEEE International Conference on Robotics and Automation, Nice, France, May 1992; 2152–2157.
- Östring M, Gunnarsson S, Norrlöf M. Closed-loop Identification of an Industrial Robot Containing Flexibilities. Control Engineering Practice. 2003; 11: 291–300.
- Moberg S, Öhr J. Robust Control of a Flexible Manipulator Arm: A Benchmark Problem. Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, July 4-8, 2005.
- Landau I, Ray D, Karimi A, Voda A, Franco A. A Flexible Transmission System as a Benchmark for Robust Digital Control. European Journal of Control. 1995; 2: 77–96.
- Reyes F, Kelly R. Experimental Evaluation of Model-based Controllers on a Direct-drive Robot Arm. Mechatronics 2001; 11: 267-282.
- Graebe S. Robust and Adaptive Control of an Unknown Plant: A Benchmark of New Format. Automatica. 1194; 30: 567–575. DOI: https://doi.org/10.1016/0005-1098(94)90142-2.
- Åström K, Hägglund T. Advanced PID Control. ISA - The Instrumentation, Systems and Automation Society, Research Triangle Park, NC, USA. 2006; ISBN:. 978-1-55617-942-6.
- Kumar PS, Subudhi B. Real-time Adaptive Control of a Flexible Manipulator using Reinforcement Learning. IEEE Transactions on Automation Science and Engineering. 2012; 9: 237–249.
- Balas MJ. Active Control of Flexible Systems. Journal of Optimization-Theory and Applications. 1978; 25: 415-436.
- Cannon RH, Schmitz E. Initial Experiments on the End-point Control of a Flexible One-link Robot. The International Journal of Robotics Research. 1984; 3: 62–75.
- Dado MHF, Soni AH. Dynamic Response Analysis of 2-R Robot with Flexible Joints. Proceedings of the IEEE International Conference on Robotics and Automation. 1987; 4: 479–483.
- Yuan K, Lin L. Motor-based Control of Manipulators with Flexible Joints and Links. Proceedings of the IEEE International Conference on Robotics and Automation. 1990; 1809–1814.
- Besseling JF, Gong DG. Numerical Simulation of Spatial Mechanisms and Manipulators with Flexible Links. Finite Elements in Analysis and Design. 1994; 18: 121–128. DOI: https://doi.org/10.1016/0168-874X(94)90096-5.
- Tokhi MO, Azad AKM. Real-time Finite Difference Simulation of a Single-link Flexible Manipulator System Incorporating Hub Inertia and Payload. Proceedings of the Institution of Mechanical Engineers. Part I: Journal of Systems and Control Engineering. 1995; 209; 21–33.
- Tokhi MO, Azad AKM. Finite Difference and Finite Element Approaches to Dynamic Modelling of a Flexible Manipulator. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. 1997; 211: 145–156.
- Yang JH, Lian FL, Fu LC. Adaptive Robust Control for Flexible Manipulators. Proceedings of IEEE Conference on Robotics and Automation. 1995; 1: 1223–1228.
- Yang JH, Lian FL, Fu LC. Nonlinear Adaptive Control for Flexible-link Manipulators. IEEE Transactions on Robotics and Automation. 1997; 13: 140–148.
- Isogai M, Arai F, Fukuda T. Modeling and Vibration Control with Neural Network for Flexible Multi-link Structures. Proceedings of IEEE Conference on Robotics and Automation. 1999; 2: 1096–1101.
- Ryu JH, Kwon DS, Park Y. A Robust Controller Design Method for a Flexible Manipulator with a Time-Varying Payload and Parameter Uncertainties. Proceedings of IEEE Conference on Robotics and Automation. 1999; 1: 413–418.
- Tokhi MO, Mohamed Z, Amin SHM, Mamat R. Dynamic Characterization of a Flexible Manipulator System: Theory and Experiments. Proceedings of IEEE Region 10 Conference TENCON, Osaka, Japan. 2000; 3: 67–172. DOI: 10.1109/TENCON50793.2020.
- Farid M, Lukasiewicz SA. Dynamic Modeling of Spatial Manipulators with Flexible Links and Joints. Computers and Structures. 2000; 75: 419–437.
- Karkoub M, Balas G, Tamma K, Donath M. Robust Control of Flexible Manipulators via m-synthesis. Control Engineering Practice. 2000; 8: 725–734. DOI:https://doi.org/10.1016/s0967-0661(00)00006-x
- Yuan K, Liu LY. Achieving Minimum Phase Transfer Function for a Noncollocated Single link Flexible Manipulator. Asian Journal of Control. 2000; 2: 179–191.
- Christoforou EG, Damaren CJ. The Control of Flexible Link Robots Manipulating Large Payloads: Theory and Experiments. Journal of Robotic Systems. 2000; 255–271.
- Benosman M, Le G. Vey. Model Inversion for a Particular Class of Nonlinear Non-minimum Phase Systems: An Application to the Two-link Flexible Manipulator. Proceedings of IEEE International Conference on Decision and Control. 2001; 2: 1174–1180.
- Kuo KY, Lin J. Fuzzy Logic Control for Flexible Link Robot Arm by Singular Perturbation Approach. Applied Soft Computing. 2002; 2: 24–38.
- Tian L, Collins C. Adaptive Neuro-fuzzy Control of a Flexible Manipulator. Mechatronics. 2005; 15: 1305-1320.
- Tian L, Fang L, Mao Z. Fuzzy Neuro Controller for a Two-link Rigid-flexible Manipulator System. Proceedings of the 9th International Conference on Neural Information Processing. 2002; 1867–1871.
- Benosman M, Le G Vey. Stable Inversion of Siso Nonminimum Phase Linear Systems Through Output Planning: An Experimental Application to the One-link Flexible Manipulator. IEEE Transactions on Control Systems Technology. 2003; 11: 588–597.
- Oke G, Istefanopulos Y. End-effector Trajectory Control in a Two-link Flexible Manipulator Through Reference Joint Angle Values Modification by Neural Networks. Journal of Vibration and Control. 2006; 12: 101–117.
- Le L, Tien A, Schaffer A, Hirzinger G. MIMO State Feedback Controller for a Flexible Joint Robot with Strong Joint Coupling. Proceedings of the IEEE International Conference on Robotics and Automation. 2007; 3824–3830.
- Khairudin M. Dynamic Modeling of a Flexible Link Manipulator Robot using AMM. Telkomnika. 2008; 6: 185-190.
- Ahmad MA, Mohamed Z, Ismail ZH. Experimental Investigation of Feedforward Control Schemes of a Flexible Robot Manipulator System. Elektrika. 2008; 10: 28–35.
- Ahmad MA, Mohamed Z, Hambali N. Dynamic Modeling of a Two-link Flexible Manipulator System Incorporating Payload. Proceedings on IEEE Conference on Industrial Electronics and Applications. 2008; 96–101.
- Roy D. Design, Modeling and Firmware of a Serial-Chain Multi-Link Direct Drive Flexible Robotic System with Sensor-Augmented Mini-Gripper: Part I. Advances in Robotics and Mechanical Engineering. 2022; 3(4): 412–423. https://doi.org/10.32474/arme.2022.03.000168

Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
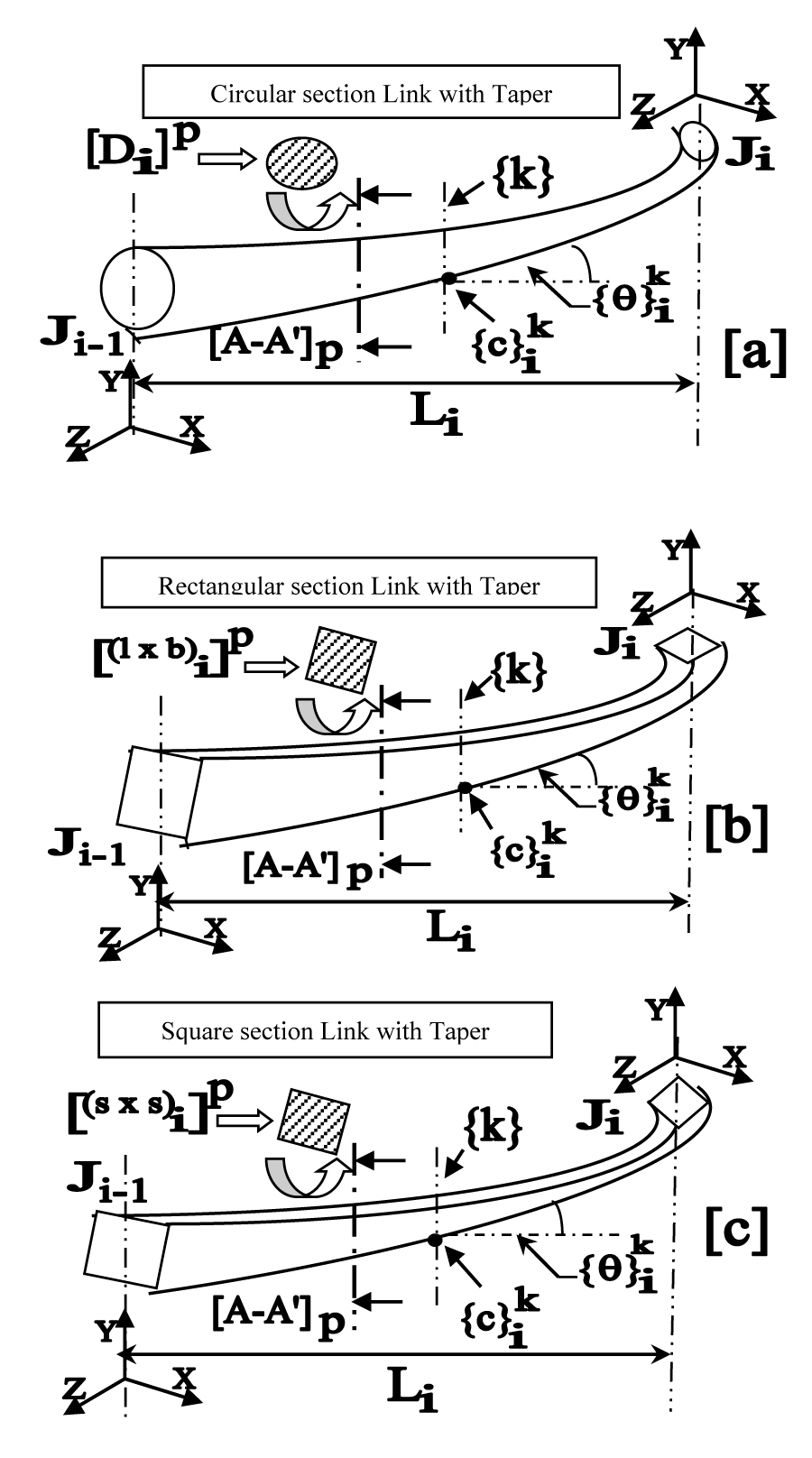
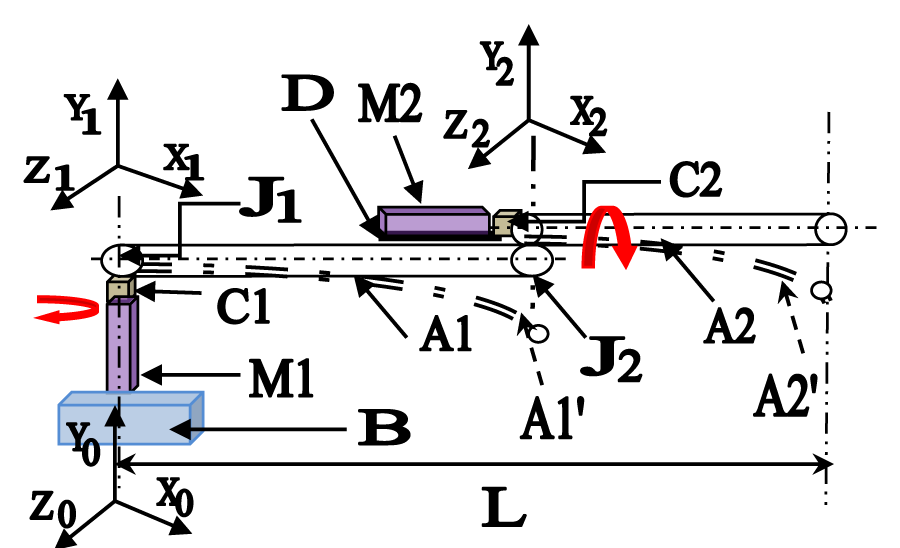
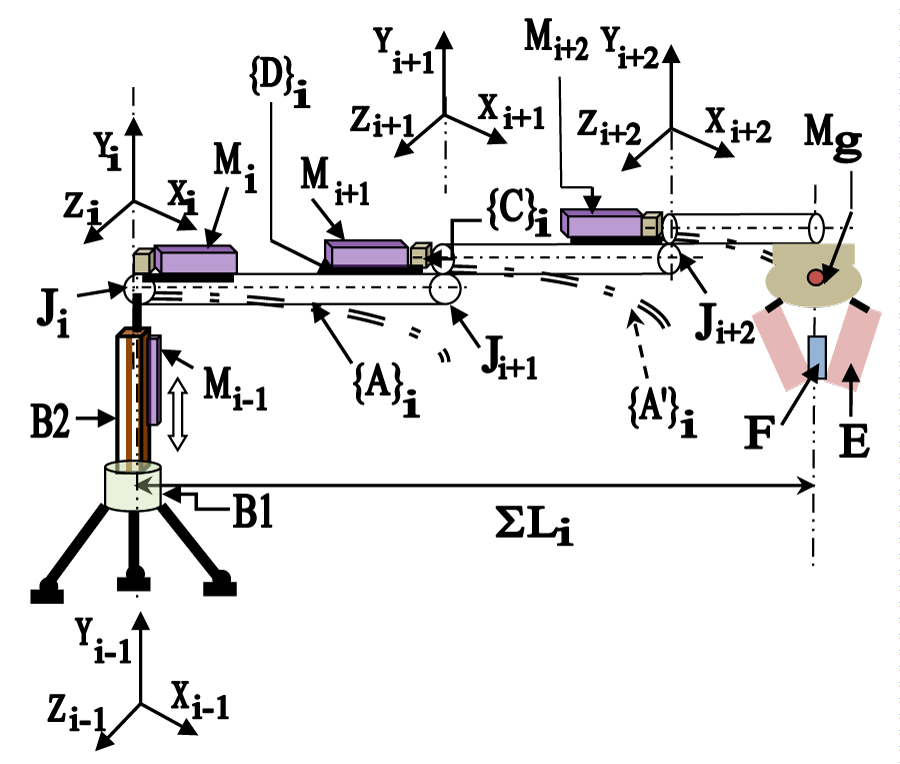
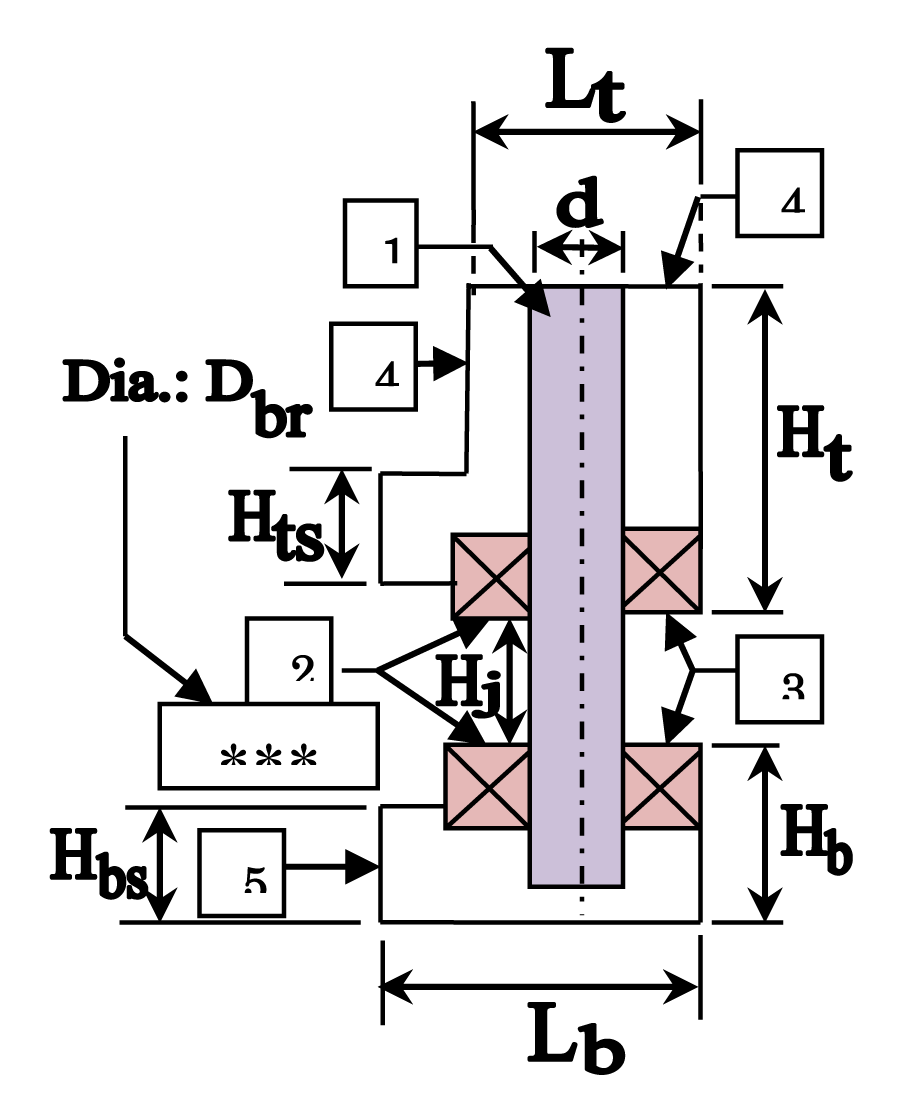
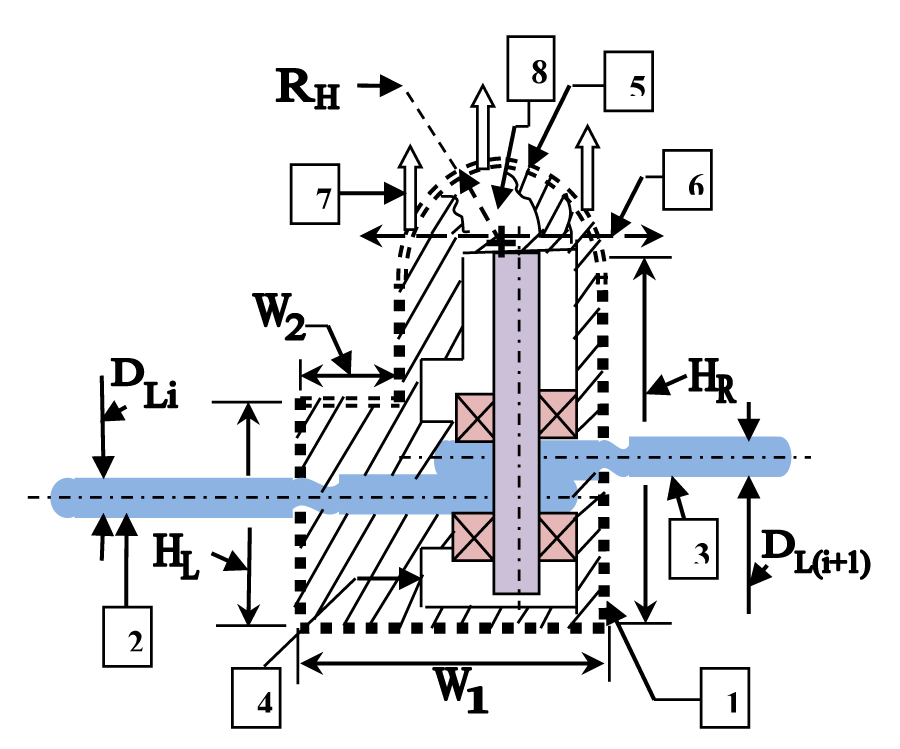
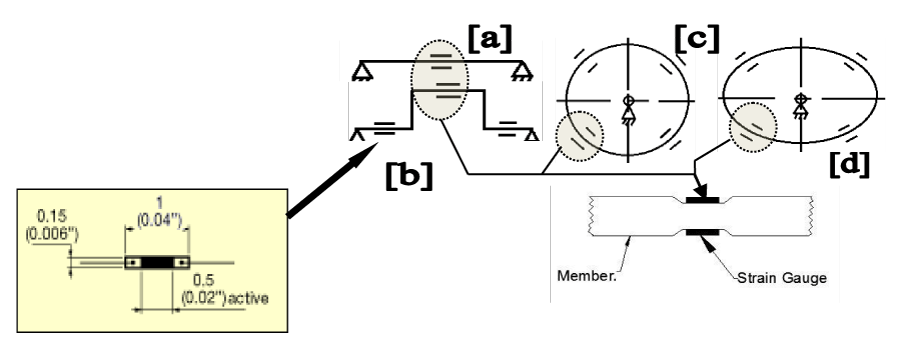





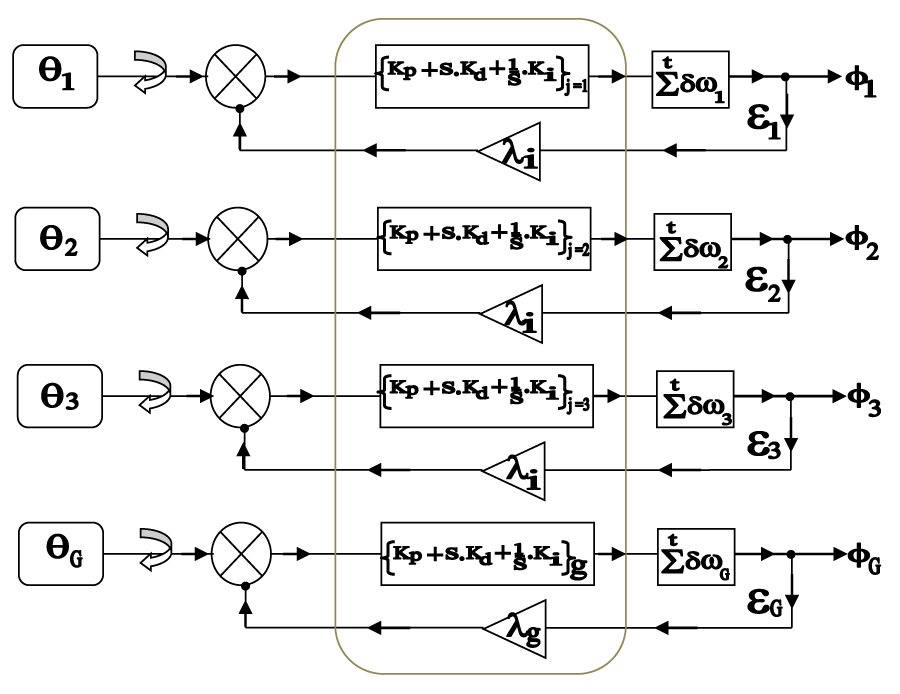
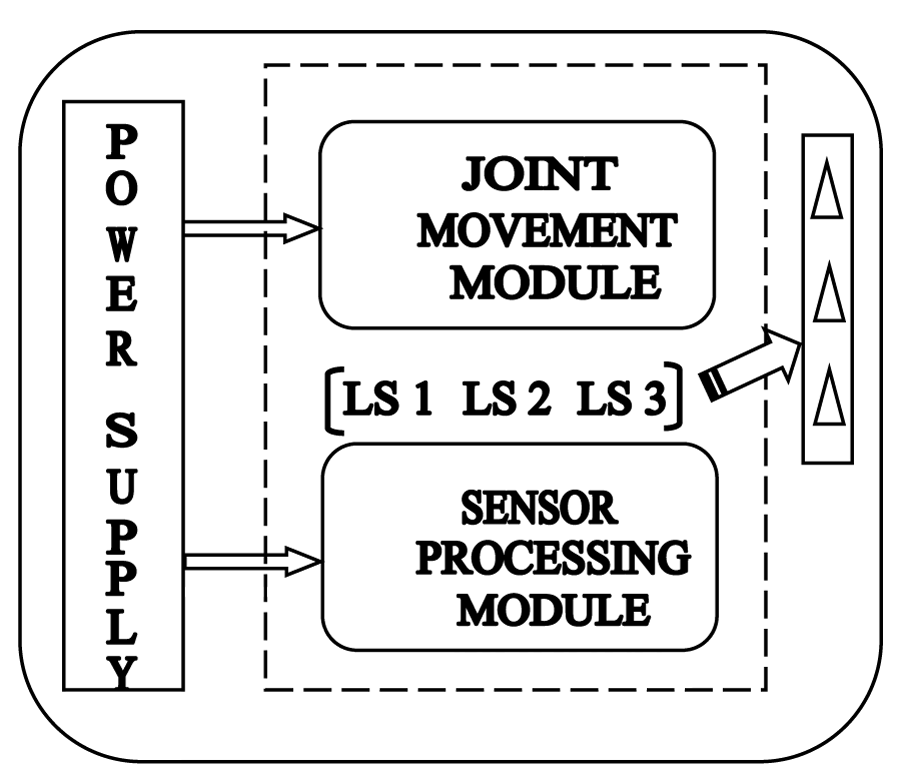
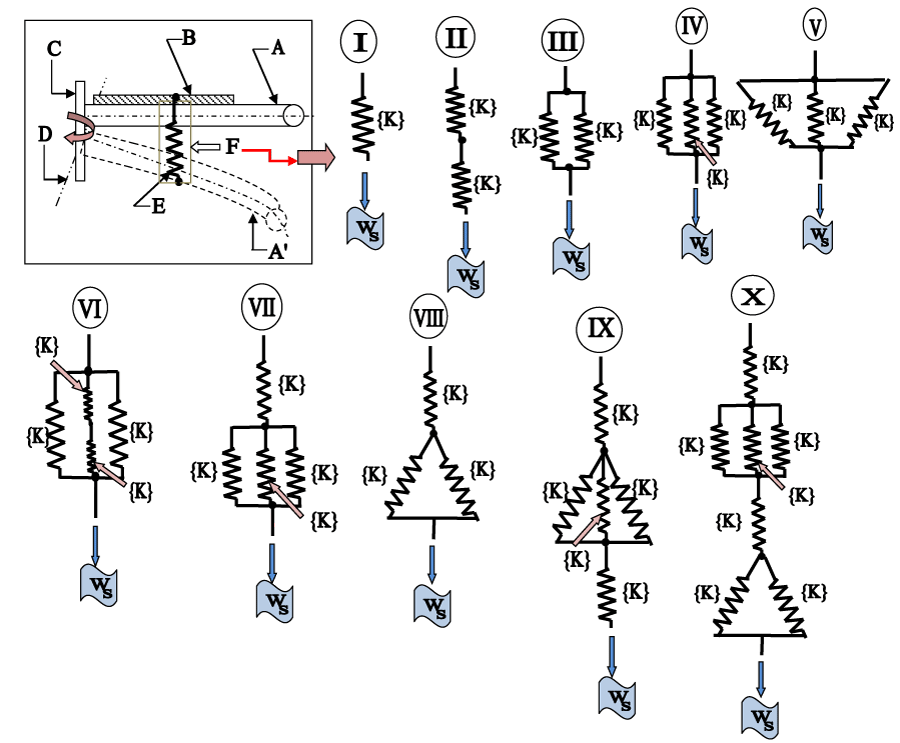

 Save to Mendeley
Save to Mendeley
