Effective moment of inertia of reinforced concrete slender beams with only tension reinforcement

For a reinforced concrete structure to be deemed satisfactory, it must satisfy both the ultimate and serviceability limits state criteria. Deflection is one of the major criteria to be satisfied under the serviceability limit state. This paper derived a model by modifying Olanitori’s model to obtain the effective moment of inertia for slender beams without compression reinforcement. The beam without compression reinforcement was subjected to a one-point load in order to determine the experimental effective moment of inertia. It was observed that the beam had an ultimate load of 83 kN. At a service load of 55.33 kN, the beam’s actual deflection was found to be 5.90 mm and the experimental effective moment of inertia, I_e(EXP) was 206.96 x10⁴mm⁴. At a service load of 55.33 kN, the estimated deflections of the beam using the proposed model P, model 1, model 2, and model 3 were 3.32 mm, 2.60 mm, 1.33 mm, and 0.78 mm respectively, while the actual deflection was 5.09 mm for the beam. From these results, the proposed model predicts more accurately the deflection of the slender beam than the three other models.

Introduction

The procedures for the design of reinforced concrete structures are based on concepts of limit states. The limit states are generally classified as ultimate limit states and serviceability limit states. The major serviceability limit states for reinforced concrete structures are caused by excessive crack widths, excessive deflections, and undesirable vibrations [1].

In practice, deflection is not normally estimated, rather deflection criterion satisfaction is based on the deemed-to-fit provision of the codes [2]. It has been noticed that buildings that were satisfactory in the deflection criterion of the service limit state, based on the deemed-to-fit provision, were known to have large cracks on the partition walls due to excessive deflections of slabs and beams [3]. The well-known equations for determining the deflection of RC members rely on computing the fractured section’s effective moment of inertia. Branson’s equation was approved by ACI-318, and it appeared in the 1971 publishing edition as a major equation for determining the effective moment of inertia in RC beam deflection calculations [4]. Since then, several arguments have been raised concerning this equation for various reasons, but most of them have centred on the model’s correctness. Designers argued that computing the troublesome cracked moment of inertia I_cr is difficult and time-consuming, especially for flanged parts. Researchers discovered that adopting Branson’s methodology resulted in a 100 percent inaccuracy in several circumstances. These reasons prompted the researchers to investigate the validity of Branson’s equation for such systems [4]. Many studies have changed this equation to make it more suitable for concrete beams with steel/FRP reinforcement [5-12].

The models for the determination of the effective moment of inertia and deflection of reinforced concrete beams from literature are the models derived from experiments conducted on beams cast using local materials of the various countries respectively. Therefore, there is a need to carry out research to determine the effectiveness of these models on reinforced concrete beams produced using our local materials in the country. The effective moment of inertia model derived from experiments carried out on beams produced from locally available materials will be able to predict deflection more accurately when compared with that from the literature.

Material and methods

The materials and methods used for this work are discussed below.

The Materials

Ordinary Portland Cement (OPC) of Dangote brand of grade 42.5 was used in this research as a binder according to ASTM C150/C150M-12 [13]. The cement was purchased in Akure metropolis of Ondo State, Nigeria. The coarse aggregate was purchased from JCC Quarry, along Akure- Owo road, it conforms to AASHTO M80-87 [14]. Also, the fine aggregate was collected from a borrowed pit from Akure metropolis, and conforms to AASHTO M6-93 [15], while fresh and clean water was used for casting and curing of the specimens. The water/cement (WC) ratio used for the experimental work was 0.6. The reinforcements used for the work were high-yield steel of 8 mm and 10 mm, with characteristic strengths of 550 N/mm² and 572 N/mm² respectively.

The experimental beams

The experimental beam was cast using the mix ratio from the trial mixes that produced concrete strength of not more than 10% lesser or greater than the targeted concrete strength.

The specimen used for this work was a rectangular beam of dimensions 100 x 150 x 750mm. The beam was without compression reinforcement but with only tension reinforcement. The total length of each beam was 750 mm and was tested under one-point loading with a 550 mm effective span.

The equipment

The equipment used for the testing of the concrete cubes and the experimental beam is the universal testing machine (UTM), shown in Figure 1.

Loading of the beams

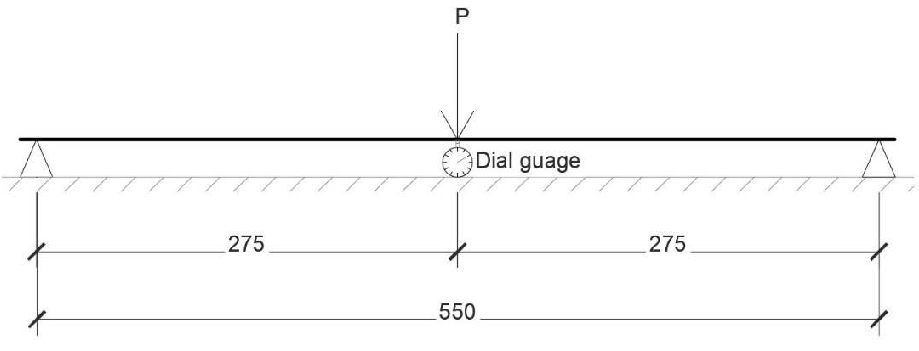
The experimental beam was simply supported, and loaded with a point load at the centre. To measure the deflection, a dial gauge was placed at the centre. The beam was loaded until failure occurs. To measure the deflection, the universal testing machine was started and stopped every 5 seconds and, read the load and the displacement from the UTM and the dial-gauge respectively. Hence, at every 5 seconds, the UTM will be stopped, then the load will be read from the machine, while the deflection will be read from the dial gauge. The stopping to take readings and starting at every 5 seconds continued until failure occurs. Figure 2 shows the schematic diagram of the beam.

Results

The deflection of the beam was measured using a dial gauge. The loading using the UTM was stopped every 5 seconds to read off the load with the corresponding deflection. The actual deflections obtained from the experimental work are presented in column 4 of Table 1.

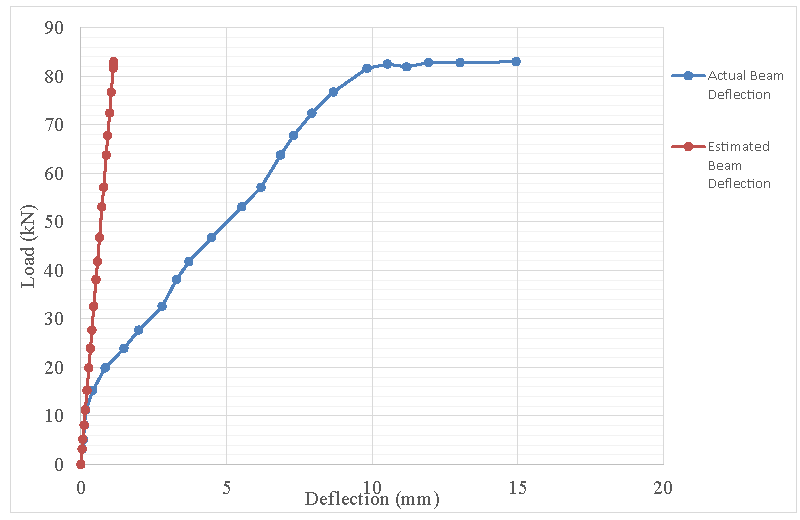
The data in Table 1 were used to plot the graph of Figure 3, from where the values of loads and deflections in between the recorded values of 5, 10, 15, 20, and 25 seconds of starting and stoppage of the loading were taken. These values taken are presented in columns 3 and 4 of Table 2.

Calculation of immediate deflection

Beams specifications and strength characteristics: The dimensions of the beam used for the work were: 100 x 150 x 750; f_cu = 11.1N/mm²; f_y = 572N/mm². The provided area of reinforcement (A_sprov) was 2Y10 bars with 157.1mm². The deflection check according to BS 8110-1 [16] was satisfactory.

Concrete’s strength characteristics such as Young’s Modulus (E_c), Moment of Resistance (M_R), Estimated Ultimate Load (P_EULT), Estimated Maximum Moment (M_Emax), and Actual Maximum Moment (M_Amax) are determined below.

E_c can be estimated from (1):

$E_c=4,725.64\sqrt{f_c^1} \left(Nm{m}^2\right)\text{ (1)}$

Where $f_c^1$ is the characteristic strength of the concrete.

$Ec=4,725.64\sqrt{11.1}=\text{ 15}.\text{7 x 1}{0}^{\text{3}}N/m{m}^2$

The moment of resistance M_ERB can be estimated by Eq. (2)

$M_{ERB}=0.87{\text{ f}}_{\text{y }}{\text{A}}_{\text{s}}*Z\text{ (2)}$

Substitute for the values of A_s, f_y, and Z, where Z= d – s/2 = 127 – 127/2 = 63.5 mm in Eq. (2)

$M_{ERB}=0.87{\text{ f}}_{\text{y }}{\text{A}}_{\text{s}}*Z=0.87 x 1000 x 157.1 x 63.5 x {10}^{-6}$

$M_{ERB}=8.68 kNm$

Since the beam is simply supported, the maximum bending moment at the centre is M = PL/4.

The estimated ultimate load for the beam can be determined thus:

$P_{EULT}=\frac{4 M_{ERB}}{L}=\frac{4 x 8.68}{0.55}=63.13 kN$

Estimated service load P_ESLT = 63.13/1.5 = 42.09 kN.

From Table 2, the actual ultimate load P_AULT = 83 kN

Actual service load P_ASLT = 83/1.5 = 55.33 kN.

The actual maximum bending moment:

$M_{AMAX}=\frac{PL}{4}=\frac{83 x 0.550}{4}=\frac{45.65}{4}=11.41 kNm$

The actual bending moment at service:

$M_{ASMAX}=\frac{PL}{4}=\frac{55.33 x 0.550}{4}=\frac{\mathrm{30.431.5}}{4}=7.6 kNm$

The estimated maximum bending moment:

$M_{EMAX}=\frac{PL}{4}=\frac{63.13 x 0.550}{4}=\frac{34.72}{4}=8.68 kNm$

The estimated bending moment at service:

$M_{EMAX}=\frac{PL}{4}=\frac{63.13 x 0.550}{4}=\frac{34.72}{4}=8.68 kNm$

Estimation of deflection for beam under estimated service load

The volume of beam = 0.75 x 0.15 x 0.1 = 0.01125 m³

Unit weight of reinforced concrete = 24 kN/m³

Dead load of beam = volume x unit weight = 0.01125 x 24 = 0.27 kN

It was built of materials with strength characteristic f_cu = 11.1 N/mm² for concrete, f_y = 572 N/mm2 for steel and concrete density γ = 2465 kg/m², Ec = 15.7 x 10³N/mm².

Check if the beam has cracked at service loads: Compute I_g for the un-cracked beam section (ignore the effect of the reinforcement for simplicity):

Beam width b_w = 100mm

I. Compute the centroid of the cross-section

$\overline{y}=\frac{h}{2}=\frac{150}{2}=75mm$

y_t = 75mm; y_b = 75mm

II. Compute the moment of inertia, I_g

$I_g=\frac{b{h}^3}{12}=\frac{100x{150}^3}{12}=2812.5 x {10}^4 \text{mm}4$

III. Determine the flexural cracking moment from Eq. (3):

$M_{cr}=\frac{f_r{I}_g}{y_t}\text{ (3)}$

Where f_r can be estimated using Eq.(4):

$f_r=0.623 {\gamma }_c \sqrt{f_c^1} MPa\text{ (4)}$

γ_{c = 1} for normal concrete and $f_c^1$ is the characteristic strength of concrete. Using Eq. (4):

$f_r=0.623 {\gamma }_c \sqrt{f_c^1}=0.623 x 1 x \sqrt{11.1}=2.08 N/m{m}^2$

In the positive moment region, using Eq. (3):

$M_{cr}=\frac{2.08x2812.5x {10}^4}{75}=780,000 N.mm=0.78 kNm$

The positivie moment at mid-span for a simply supported beam with point load = wl/4

$\text{Dead load moment}= \frac{0.27 x 0.55}{4}=0.037 kNm <M_{cr}=0.78 kNm$

Hence, section not cracked

$\begin{array}{l}Dead plus live load M_{EDL+LL}= \frac{\left(42.09+0.27\right) x 0.55}{4}\\ =5.82 kNm>M_{cr}=0.78 kNm\end{array}$

Hence the section has cracked.

Therefore, it will be necessary to compute I_cr and I_e at the mid-span.

Compute I_cr at midspan. It is known that the beams have rectangular sections

Beam without compression steel

$I_{cr}=\frac{b{k}^3{d}^3}{3}+nAs{(d-kd)}^2\text{ (5)}$

$kd=\frac{\sqrt{2dB+1}-1}{B}\text{ (6)}$

Where:

$n=\frac{E_s}{E_c}=\frac{200}{15.7}=12.74$

$B=\frac{b}{n{A}_s}=\frac{100}{12.74 x 157.1}=\frac{100}{2001.5}=0.05mm$

From Eq. (6) the value of kd can be determined as shown below for the beam without compression reinforcement:

$kd=\frac{\sqrt{2x127x0.05+1}-1}{0.05}$

$kd=\frac{\sqrt{13.7}-1}{0.05}$

$kd=\frac{3.70-1}{0.05}$

$c=kd=\frac{2.7}{0.05}=54mm$

$k=\frac{54}{127}=0.425$

k=54/127=0.425

The crack moment of inertia can be determined using Eq.(5)

$I_{cr}=\frac{100 x {0.425}^3 x {127}^3}{3}+12.74 x 157.1{(127-0.425 x 127)}^2$

$I_{cr}=524.15 x{10}^4+ 2001.5{(73.02)}^2$

$I_{cr}=524.15 x{10}^4+ 2001.5(5332.92)$

$I_{cr}=524.15 x{10}^4+1067.18 x{10}^4$

$I_{cr}=1591 x{10}^4 \text{mm}4$

Therefore, I_cr at mid-span for the beam with only Tension reinforcement = 1591×104mm⁴

[For SI unit, where Es = 200 kN/mm² and Ec = 15.7 kN/mm²]

Compute immediate dead-load deflection: When the load acting on the beam is less than the cracking load (M_a< M_cr), the section is uncracked therefore I_e = I_g

I. Compute I_e at mid-span

Because M_ESMAX = 5.79 kNm is greater than M_cr = 0.78 kNm, hence the section is cracked and I_e must be determined by using Eq.(7).

$I_e={\left(\frac{M_{cr}}{M_a}\right)}^3{I}_g+\left[1-{\left(\frac{M_{cr}}{M_a}\right)}^3\right]I_{cr}\text{ (7)}$

$\begin{array}{l}{M}_a=\frac{wl}{4};where w=unfactored live load; \\ M_a=\frac{42.36 x 0.55}{4}=5.82 kNm\end{array}$

Therefore:

${\left(\frac{M_{cr}}{M_a}\right)}^3={\left(\frac{0.78}{5.82}\right)}^3={\left(75.91 x {10}^{-6}\right)}^3=0.002\approx 0$

We have:

$\begin{array}{l}{I}_e=0 x 2812.5 x {10}^4+\left(1-0\right)x 1591x{10}^4\\ =1591 x {10}^4 m{m}^4=I_{cr}<I_g\end{array}$

II. Compute I_e at mid-span for the beam with compression reinforcement

Because M_EDL+LL = 5.82 kNm is greater than M_cr = 0.78 kNm, hence the section is cracked and I_e must be determined by using Eq.(7):

$I_e={\left(\frac{M_{cr}}{M_a}\right)}^3{I}_g+\left[1-{\left(\frac{M_{cr}}{M_a}\right)}^3\right]I_{cr}\text{ (7)}$

Therefore:

${\left(\frac{M_{cr}}{M_a}\right)}^3={\left(\frac{0.78}{5.82}\right)}^3={\left(75.91 x {10}^{-6}\right)}^3=0.002\approx 0$

We have:

$I_e=0 x 2812.5 x {10}^4+\left(1-0\right)x 2621.91x{10}^4=2621.91 x {10}^4 m{m}^4=I_{cr}<I_g$

III. Compute estimated immediate dead load deflection: Since it assumed that the beam behaved like a simply supported beam with a concentrated load at the centre, the mid-span deflection can be estimated using Eq.(8) below.

$\Delta =\frac{w{l}^3}{48EI}\text{ (8)}$

Eq.(8) is the general equation for the estimation of deflection for beams without compression reinforcement and it can be derived as follows:

Substituting for the values of E_c, l, and I = I_e in Eq. (8), we have:

${\Delta }_{max}=\frac{w{l}^3}{48E{I}_e}=\frac{w x {550}^3}{ 48 x15.7x {10}^3 x 1591 x {10}^4 }=\frac{w{l}^3}{48EI}$

${\Delta }_{max}=\frac{w{l}^3}{48E{I}_e}=\frac{w 1.664 x {10}^8}{ 1.22 x {10}^{13} }$

${\Delta }_{max}=\frac{w{l}^3}{48E{I}_e}=1.36w x {10}^{-5}mm\text{ (9)}$

Using Eq. (9), the estimated mid-span deflection for the beams was determined. The results obtained are presented in column 5 of Table 3.

The estimated deflection is lesser than the actual deflection. The ultimate beam load was 83 kN, and the service load is about 66.66% of the ultimate load and which equals 55.33 kN for the beam. From Figure 3, the corresponding estimated deflection for a service load of 55.33 kN is 0.75 mm, while the corresponding actual deflection is 5.90 mm. From Table 3, column 4, the actual deflection increases as the load increases. Also from Figure 3, the actual load-deflection curve is not linear, and deflection increases as load increases. At the beam’s ultimate load of 83 kN, the deflection curve flattened out and the collapse of the beam took place. Column 5 of Table 3 and Figure 3, shows the estimated deflection, which increases with the load and linear throughout. Column 6 of Table 3 shows how much the actual deflection exceeded the estimated deflection. At the service load of 55.33 kN, the difference between the estimated and actual deflection is 687%. From the above, I_e used in the computation of the estimated deflection is grossly inaccurate. Since the estimated deflection is lesser than the actual deflection, indicates that I_e is overestimated.

Determination of Experimental I_cr(exp)

The deflection at mid-span, of the beam and load case is calculated using equation (8) repeated below:

${\Delta }_{max}=\frac{w{l}^3}{48E{I}_e}$

Taking E = E_C, an experimental effective moment of inertia, I_e(exp) can be worked out using Equation (9) by substituting maximum deflection (∆_max) with measured deflection (∆_ACT) as given by Equation (11).

$I_{e(EXP)}=\frac{w{l}^3}{48E_c{\Delta }_{ACT}}\text{ (10)}$

Substituting the values of l and E_c into Eq. (10), we have:

$I_{e(EXP)}=\frac{w{550}^3}{48 x 15.7x{10}^{3}x{\Delta }_{ACT}}$

$I_{e(EXP)}=\frac{w1.664 x{10}^8}{7.54x{10}^{5}x{\Delta }_{ACT}}=220.69\frac{w}{{\Delta }_{ACT}}\text{ (11)}$

Using Eq. 11, I_e(exp) is determined and presented in Column 4 of Table 4.

At a service load of 55.33 kN and actual deflection of 5.90 mm, the experimental effective moment of inertia, I_e(exp) = 206.96 x10⁴mm⁴

Discussion

The main aim of this work is to develop a model that will be able to predict the deflection of beams produced from locally available materials more accurately than the ones from the literature.

Proposed model

The proposed model is based on Olanitori’s model [3], which is presented here as Equation (12).

$I_e={\left(\frac{M_{cr}}{M_a}\right)}^3{I}_g+\left[1-{\left(\frac{M_{cr}}{M_a}\right)}^3\right]\alpha I_{cr}\text{ (12)}$

Where α the experimentally determined reduction is a factor, and equals 0.24.

In the proposed model α is replaced with β. Thus the model is in the form of Equation (13).

$I_e={\left(\frac{M_{cr}}{M_a}\right)}^3{I}_g+\left[1-{\left(\frac{M_{cr}}{M_a}\right)}^3\right]\beta I_{cr}\text{ (13)}$

Where:

β: Experimentally determined reduction factor

$206.96 x{10}^4 ={\left(\frac{M_{cr}}{M_a}\right)}^3{I}_g+\left[1-{\left(\frac{M_{cr}}{M_a}\right)}^3\right]\beta I_{cr}$

Where β is the reduction factor for the effective moment of inertia I_e.

Therefore:

${\left(\frac{M_{cr}}{M_a}\right)}^3={\left(\frac{0.78 x {10}^3}{5.8 x {10}^3}\right)}^3= 2.43 x {10}^{-3}\approx 0$

Since we are interested in the deflection at the service load, then, I_e(EXP) = 206.96 x10⁴mm⁴ at service load 55.33kN.

We have a crack moment of inertia I_cr to be:

$I_{\text{cr} }{=}_{ }\text{1591}\times \text{1}{0}^{\text{4}}{\text{mm}}^{\text{4}}$

$206.96 x{10}^4=0 x 2812.5 x {10}^4+\left(1-0\right)x1591 x{10}^4 \beta$

$206.96 x{10}^4=0 +1591 x{10}^4 \beta$

Therefore

$\beta =\frac{ 206.96 x{10}^4}{1591*{10}^4}=0.130$

${\Delta }_{pmax}=\frac{w{l}^3}{48E_c \beta I_e}=\frac{w x {550}^3}{48 x 15.7 x{10}^{3}x0.130 x 2812 x{10}^4}$

${\Delta }_{pmax}=\frac{w x {550}^3}{48 x 15.7 x{10}^{3}x0.130 x 2812 x{10}^4}=0.00006w mm\text{ (14)}$

Other existing models

Model 1: Akmaluddin and Thomas Model [16]

$I_e=I_{cre}+\left(I_g-I_{cre}\right)e^{\varnothing }\text{ (15)}$

Where:

$\begin{array}{l}{I}_{cre}=\left(0.1618+0.0418n\rho \right)\frac{b{h}^3}{12}=\\ \left(0.1618+0.0418x12.74x0.0124\right)\frac{100x{150}^3}{12}\end{array}$

$I_{cre}=\left(0.1618+0.0066\right)x2812.5x{10}^4=473.62x{10}^4$

$\varnothing =-\left(\frac{M_a}{M_{cr}}\right)\left(\frac{L_{cr}}{L}\right)\left(8.474-9.0607\rho +2.842{\rho }^2\right)$

$L_{cr}=L\left(1-\frac{M_{cr}}{M_a}\right)$

$L_{cr}=550\left(1-\frac{0.78 x {10}^3}{5.8 x {10}^3}\right)=476.04 mm$

$\begin{array}{l}\varnothing =-\left(\frac{5.8 x {10}^3}{0.78 x {10}^3}\right)\left(\frac{476.04}{550}\right)\\ \left(8.474-9.0607x0.0124+2.842x{0.0124}^2\right)\end{array}$

$\varnothing =-6.440\left(8.474-0.1124+0.00044\right)=-53.85$

$\begin{array}{l} I_e=I_{cre}+\left(I_g-I_{cre}\right)e^{\varnothing }=\\ 473.62x{10}^4+\left(2812.5x{10}^4-473.62x{10}^4\right)e^{-53.85}\end{array}$

$\begin{array}{l}{I}_e=473.62x{10}^4+\left(2338.9x{10}^4\right)e^{-53.8}\\ =473.62x{10}^4+9.60x{10}^{-17}\end{array}$

$I_e=473.62x{10}^4 m{m}^4$

$\begin{array}{l}{\Delta }_{1max}=\frac{w{l}^3}{48E_c{I}_e}=\frac{w x {550}^3}{48 x 15.7 x{10}^3 x 473.62 x{10}^{4 }}\text{ (16)}\\ =0.000047 w mm\end{array}$

Model 2: Ammash and Muhaisin Model [7]

$I_e={\left(\frac{M_{cr}}{M_a}\right)}^{\left(\epsilon +\gamma \right)}*I_g+\left[\left(\left(\epsilon +\gamma \right)-{\left(\frac{M_{cr}}{M_a}\right)}^{\left(\epsilon +\gamma \right)}\right)\right]I_{cr}*\left(\epsilon +\beta \right) \text{ (17)}$

Where:

$\begin{array}{l}\beta =\frac{{\rho }^1}{\rho }; \gamma =f_l-\frac{\left({\rho }^1+\alpha \rho \right)n}{\mu }; \\ \alpha =5.26-0.525\left(\frac{d}{b_w}\right); \mu =\frac{I_g}{I_{cr}}; \epsilon =\frac{H}{L}\end{array}$

f_l – factor depending on loading type such as:

Distributed load =1.25; 2. Two-point load =1.0 and 3. Concentrated load =0.75

$\begin{array}{l}\alpha =5.26-0.525\left(\frac{127}{100}\right)=6.01; \\ \mu =\frac{I_g}{I_{cr}}=\frac{2812.5x{10}^4}{1591 x{10}^4}=1.77\end{array}$

$\rho =\frac{A_s}{bd}=\frac{157.1}{100 x 127}=0.0124$

ρ¹ is the reinforcement ration at the compression area

ρ is the reinforcement ration at the tension area

ρ^1/ρ=0.0124/0.0124=1; ε=H/L=150/550=0.27

$\begin{array}{l}\gamma =f_l-\frac{\left({\rho }^1+\alpha \rho \right)n}{\mu }=0.75-\\ \frac{\left(0.0124+6.01x0.0124\right)12.74}{1.77}=0.12\end{array}$

$\begin{array}{l}{I}_e={\left(\frac{0.78 x {10}^3}{5.8 x {10}^3}\right)}^{\left(0.27+0.12\right)}x2812.5x{10}^4+\\ \left[\left((0.27+0.12)-{\left(\frac{0.78 x {10}^3}{5.8 x {10}^3}\right)}^{\left(0.27+0.12\right)}\right)\right]1591 x{10}^{4}x\left(0.27+1\right)\end{array}$

$\begin{array}{l} I_e={0.0135}^{0.39}x2812.5x{10}^4+\\ \left[\left(0.39\right)-{0.0135}^{0.39}\right]1591 x{10}^{4}x1.27\end{array}$

$\begin{array}{l}{I}_e=1.87 x{10}^{-1}x2812.5x{10}^4\\ +\left[\left(0.39\right)-0.187\right]1591 x{10}^{4}x1.27\end{array}$

$I_e=525.94x{10}^4+\left[0.203\right]1591 x{10}^{4}x1.27=936.12x{10}^4$

$\begin{array}{l}{\Delta }_{2max}=\frac{w{l}^3}{48E_c{I}_e}=\frac{w x {550}^3}{48 x 15.7 x{10}^3 x 936.12 x{10}^{4 }}\text{ (18)}\\ =0.000024 w mm\end{array}$

Model 3: Bischoff’s Model [12]

$\frac{1}{l_e}={\left(\frac{M_{cr}}{M_a}\right)}^m \frac{1}{I_g}+ \left[1- {\left(\frac{M_{cr}}{M_a}\right)}^m\right] \frac{1}{I_{cr}}\text{ (19)}$

Substituting for the values of I_g = 2812×10⁴ mm⁴, I_cr = 1591×10⁴ mm⁴, M_cr = 0.78×10³_NM, M_a = 5.8×10³ NM and m = 2, we have:

$\frac{1}{l_e}={\left(\frac{0.78 x {10}^3}{5.8 x {10}^3}\right)}^{2}x \frac{1}{2812.5x{10}^4}+\left[1-{\left(\frac{0.78 x {10}^3}{5.8 x {10}^3}\right)}^2\right]x\frac{1}{1591 x{10}^4}$

$\frac{1}{I_e}=0+\left[1-0\right]x\frac{1}{1591 x{10}^4}=\frac{1}{1591 x{10}^4}$

$I_e=1591 x{10}^{4}mm$

$\begin{array}{l}{\Delta }_{3max}=\frac{w{l}^3}{48E_c{I}_e}=\frac{w x {550}^3}{48 x 15.7 x{10}^3 x 1591 x{10}^{4 }}\text{ (20)}\\ =0.000014 w mm\end{array}$

Comparative analysis of the models

The proposed model (model P), model 1, model 2, and model 3 were used to estimate the deflection of the beam. The results of the estimation were presented in Table 5. For the beam at a service load of 55.33 kN, the estimated deflections using model P, model 1, model 2, and Model 3 are 3.32 mm, 2.60 mm, 1.33 mm, and 0.78 mm respectively. The percentage differences between these deflections to the actual deflection of 5.09 mm at the service load are 53.31%, 95.77%, 282.71%, and 552.56% respectively.

Conclusions and recommendations

Based on the analysis and comparison of the different models of estimating deflection, the following conclusions and recommendations were made:

Conclusion

The actual deflection of the experimental beam at service load was 5.90 mm which exceeded the maximum permissible computed deflections (ACI 318, 2005) of L/480, which equals 1.15 mm. Therefore, non-structural elements, such as partition walls, supported by such beams are likely to be damaged by large deflections, and therefore the beam is not satisfactory in deflection. Models P, 1, 2, and 3 grossly underestimated the deflection by 53.31%, 95.77%.282.71%, and 552.56% respectively.

Recommendation

The recommendations made are as follows:

1. Research should be done on the effect of tension reinforcement sizes on the effective moment of inertia and deflection of reinforced concrete slender beams.
2. More research should be conducted on the effect of compression reinforcement on the effective moment of inertia and deflection of reinforced concrete slender beams so that more accurate estimated deflection can be achieved.
3. The span/effective depth ratio alone should not be used in checking for deflection, rather this should be complemented by actual deflection calculation.

1. Wight JK, MacGregor JG. Reinforced concrete mechanics and design: Fifth Edition. Prentice Hall: Pearson Education International. 2009.
2. Nkuma L. Effectiveness of BS 8110 Control Measures on Deflection at Service. 500 L Seminar, Federal University of Technology, Akure, Ondo State, Nigeria. 2013.
3. Olanitori LM. Effective Moment of Inertia of Single-Spanned Reinforced Concrete Beams with Fixed Beam-Column Joints. Journal of Civil Engineering and Urbanism. 2019; 9(2): 07-16.
4. Ammash HK, Hemzah SA, Al-Ramahee MA. Unified Advanced Model of Effective Moment of Inertia of Reinforced Concrete Members. International Journal of Applied Engineering Research. 2018; 13(1):557-563
5. Al-Zaid RZ, Al-Shaikh AH, Abu-Hussein M. Effect of Loading Type on the Effective Moment of Inertia of Reinforced Concrete Beams. ACI Structural Journal. 1991; 88(2): 184-190.
6.  Fikry AM, Thomas C. Development of a Model for the Effective Moment of Inertia of One-Way Reinforced Concrete Elements. ACI Structural Journal. 1998; 95(4): 444-455.
7. Ammash HK, Muhaisin MH. Advanced Model for the Effective Moment of Inertia Taking into Account Shear Deformations Effect. Al-Qadisiyah Journal for Engineering Sciences. 2009; 2(2): 108–28.
8. Muhammad Masood R, Nadjai A. Evaluation of ACI 440 Deflection Model for Fiber-Reinforced Polymer Reinforced Concrete Beams and Suggested Modification. ACI Structural Journal. 2009; 106(6): 762-71.
9. Hall T, Ghali A. Long-Term Deflection Prediction of Concrete Member Reinforced with Glass Fiber Reinforced Polymer Bars. Can J Civ Eng. 2000; 27:890-898
10. Faza SS, GangaRao HVS. Pre-and Post-Cracking Deflection Behaviour of Concrete Beams Reinforced with Fibre-Reinforced Plastic Rebars. In Proceedings of the First International Conference on Advance Composite Materials in Bridges and Structures (ACMBS-I), Canadian Society of Civil Engineers, Sherbrooke, Canada. 1992; 129–37.
11. Benmokrane B, Chaallal O, Masmoudi RT. Flexural Response of Concrete Beams Reinforced with FRP Reinforcing Bars. ACI Structural Journal. 1996; 93(1): 46–55.
12. Bischoff PH. Re-evaluation of Deflection Prediction for Concrete Beams Reinforced with Steel and Fiber Reinforced Polymer Bars. Journal of Structural Engineering. ASCE. 2005; 131(5): 752-762.
13. ASTM C150/C150M-12. Standard specification for portland cement. ASTM International. 2012; i:1–9. https://doi.org/10.1520/C0150
14. AASHTO M80-87. Standard Specification for Coarse Aggregates for Portland Cement Concrete. The American Association of State Highway and Transportation. 1999; 60-62.
15. AASHTO M6-93. Standard Specification for Fine Aggregate for Portland Cement Concrete. The American Association of State Highway and Transportation. 1997; 1-3.
16. BS 8110-1. Structural Use of Concrete – Part 1: Code of Practice for Design and Construction. British Standards Institution, London. 1997.
17. Akmaluddin A, Thomas C. Experimental Verification of Effective Moment of Inertia Used in the Calculation of Reinforced Concrete Beam Deflection. in Proceedings of the International Civil Engineering Conference “Towards Sustainable Civil Engineering Practice. Surabaya, Indonesia. 2006.