Study on the mechanical properties of anisotropic red sandstone under point load strength test and uniaxial compression strength

The red sandstone of Xiaopu 3# branch Cave in the Yuxi section of the Central Yunnan Water Diversion Project was taken as the research object. The uniaxial compression strength and point load strength test are conducted from the perspectives of vertical and parallel stratifications, respectively, and then the anisotropy of red sandstone was analyzed in detail. The data obtained from the field and laboratory test was analyzed, and the conversion relationship between point load strength index and uniaxial compression strength is a power function under both parallel stratification and vertical stratification. The study results showed that: The mechanical properties of red sandstone have obvious anisotropy. The difference in its mechanical properties is particularly evident in UCS and point load tests and I_s(50) and UCS under vertical stratification are significantly greater than I_s(50) under parallel stratification. The point load strength correction index m of red sandstone is m = 0.4096 under parallel stratification, and m = 0.4408 under vertical stratification.

Abbreviations

PRC: The People’s Republic of China; CYWD Project: Central Yunnan Water Diversion Project; ASTM: American Society for Testing and Materials; ISRM: International Society for Rock Mechanics; UCS: Uniaxial Compressive Strength; PLT: Point Load Test; I_s(50): Point load strength index; R²: Correlation coefficient

Introduction

UCS is one of the most important strength parameters of rocks in geotechnical engineering design [1-3], and UCS is also widely used in the basic classification of rock mass, the determination of the engineering rock mass level [2,4], the assessment of engineering geological and so on, which has an important reference value for the safety and stability of mine engineering, underground engineering, slope, and ground foundation engineering[1-3,5,6]. The UCS test requires the preparation of the standard rock samples [7,8], and the samples are only can be tested in the laboratory according to the standards such as ISRM [9] and ASTM [10]. There are some limitations [7] in the number, type, and preparation of samples, so the UCS test became more difficult [8], especially for the preparation of the samples for soft rocks and highly weathered rocks. Consequently, the construction of a practical field test method to replace the UCS test has been an important target for researchers. PLT is one of the indirect methods to estimate the UCS of rock [11], which is widely applied in rock engineering and geotechnical engineering [12] owing to the point load tester being portable, the test is easy and low cost. The sample of PLT can be easily prepared in the field or laboratory, and the rock samples can be cylindrical, massive, or irregular [13]. PLT is usually utilized to test irregular samples and also solve other thorny problems in routine test due to its convenience and efficiency, so PLT has been widely used in the engineering site [14].

Protodyakonov [15] first put forward the idea of PLT with irregular blocks, then D’Andrea [16] and Franklin [17] studied the transformation between rock’s I_s(50) and UCS. At present, there are three main conversion relational functions between sandstone I_s(50) and UCS: the zero intercept linear function, the non-zero intercept linear function, and the power function, as shown in Table 1.

Many researchers have studied the correction index m. Wong, et al. [33] studied the granite samples with different weathering degrees, finding that the actual correction index m obtained by the regression of strength data of samples with different sizes was quite different from its recommended value in the specification. Yin, et al. [34] also found that in the size correction function, the correction index value m of slightly-weathered granite was around 0.443 - 0.600, and that of moderately-weathered granite was between 0.545 - 5.562. Li, et al. [35] used different loading methods (axial test and diametral test) to carry out the PLT and obtained a correction index of 0.5. Yao, et al. [36] conducted both the PLS test and UCS test on rock samples with vertical and parallel stratifications respectively, revealing that the correction index of gneiss was m = 0.44 under vertical stratification and m = 0.42 under parallel stratification. Dai, et al. [32] carried out the axial tests on three disc-shaped samples with different coring diameters and obtained the results that the correction indexes m of marbles and red sandstones were 0.44 and 0.53 respectively.

At present, different researchers keep different conclusions about the empirical relationship and the correction index m between I_s(50) and UCS. Particularly, the relationship between I_s(50) and UCS of anisotropic rock need to be further investigated.

Previous research findings predominantly center around sandstone, with a limited number of studies conducted on red sandstone [5,37]. In this study, the red sandstone of Sinian Chengjiang Group retrieved from the downstream of Xiaopu 3# branch Cave in the Yuxi section of the CYWD Project was taken as the research object. From the perspectives of parallel and vertical stratification, the UCS and the multiple sizes PLT are conducted respectively, and the mechanical properties are analyzed in detail. The empirical relationship between I_s(50) and UCS and the reference value of correction index m were obtained from red sandstone, and these characteristics critically affect the safety of in Yuxi section of the CYWD Project [38], which is under construction, and represent urgent engineering problems that hinder efficient construction. Therefore, establishing the conversion relation between I_s(50) and UCS of red sandstone is a challenging but worthwhile undertaking.

Study area and material

Study area

In this study, the red sandstone of Sinian Chengjiang Group retrieved from the downstream of Xiaopu 3# branch Cave in Yuxi section of the CYWD Project was taken as the research object. The samples’ location is E 102 42’24.92 “, N 24 35” 4.43 “, and the rock sample is purple-red. According to the rock ore identification, fine-extremely fine-grained feldspar-quartz sandstone contains a small amount of very fine sand, silt composition contains quartz, feldspar, eruptive rock, aphanite, quartzite, chert, dolomite and other components. The composition of sandstone is complex, including quartz 81%, feldspar 10.5%, eruptive rock 1.0%, aphanite 1.5%, quartzite 2.0%, chert 2.5%, dolomite 14.0%, and the orthogonal polarimetric photograph of the sandstone microscope is shown in Figure 1.

Figure 1: Microscopic analysis of the sample under a microscope.

Uniaxial compressive strength test

Prepared by the automatic double-blade rock-core cutting machine (SCQ-4A), the diameter of the cylindrical core sample is set to 43.493 - 109.42 mm, the length of the core is 58.25 - 103.62 mm, and the aspect ratio is defaulted as 0.877 ~ 2.084. Following the ISRM [9] standard, red sandstone is tested, and its average value is taken as the UCS of the sample (Table 2). According to ISRM [39], the aspect ratio of UCS is 2.0 (50 mm × 100 mm). However, if the length diameter ratio is not 2.0, the USC is corrected on the basis of Eq. 1 [40]. During the test, both ends of the sample must be smooth and flat. The sample is loaded by the electro-hydraulic pressure tester (HYE - 2000), the loading rate is controlled within the range of 1,000 - 2,000 N/s, and the maximum loading capacity is set to 2,000 kN. The processing and testing of the red sandstone core are shown in Figure 2.

Figure 2: Test process of rock samples. (a) The rock core samples were taken from the field, (b) The processed rock core sample, (c) Test process of UCS, and (d) The rock core samples after the test.

$UCS=\frac{0.8668UC{S}^{*}}{0.778+\frac{0.222}{L/D}}\text{ (1)}$

Where L is length, D is diameter, and UCS* is the UCS of the specimen at a ratio of L/D.

Point load test index

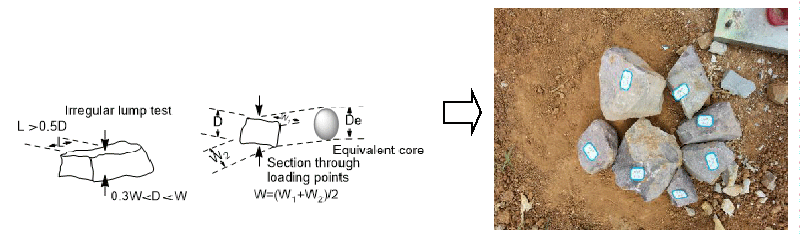
PLTs of irregular blocks were carried out on red sandstone samples, as shown in Figure 3.

Figure 3: PLTs of irregular blocks.

The irregular specimen can be calculated by the method of equivalent core diameter, and the I_s(50) is determined by ASTM [41] and standards [23] as Eq. 2-5:

$D_e^2=\frac{4\cdot W\cdot D}{\pi }\text{ (3)}$

$I_s=\frac{P}{D_e^2}\text{ (3)}$

$I_{\text{S(50)}}=I_S\cdot F\text{ (4)}$

$F={\left(\frac{D_e}{50}\right)}^{{}^m}\text{ (5)}$

Where P is the failure load and De is the equivalent diameter of irregular blocks, D and W are the maximum lengths and average width of the failure surface in millimetres, m is the correction index.

Various sizes of rock samples were selected for the PLT, and the results were corrected by Eq. 2-5. The results showed that I_s(50) under vertical stratification is significantly greater than I_s(50) under parallel stratification, and the point load strength of red sandstone has obvious anisotropy. This obvious difference of strength can be expressed by the point load strength anisotropy index β, and β = I’_s(50) / I”_s(50) =2.31 (I’_s(50) is the point load strength index of vertical stratification, and I”_s(50) is the point load strength index of parallel stratification).

Result and discussion

The calculation of the correction index

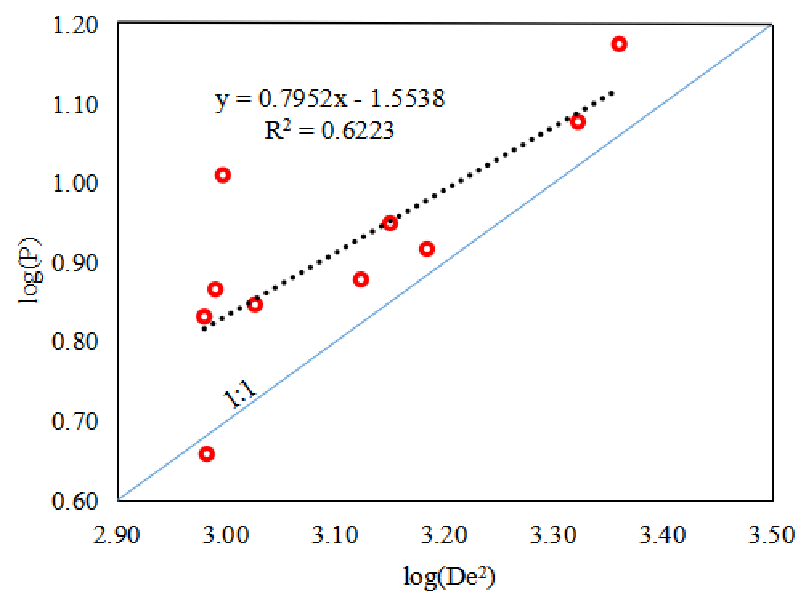
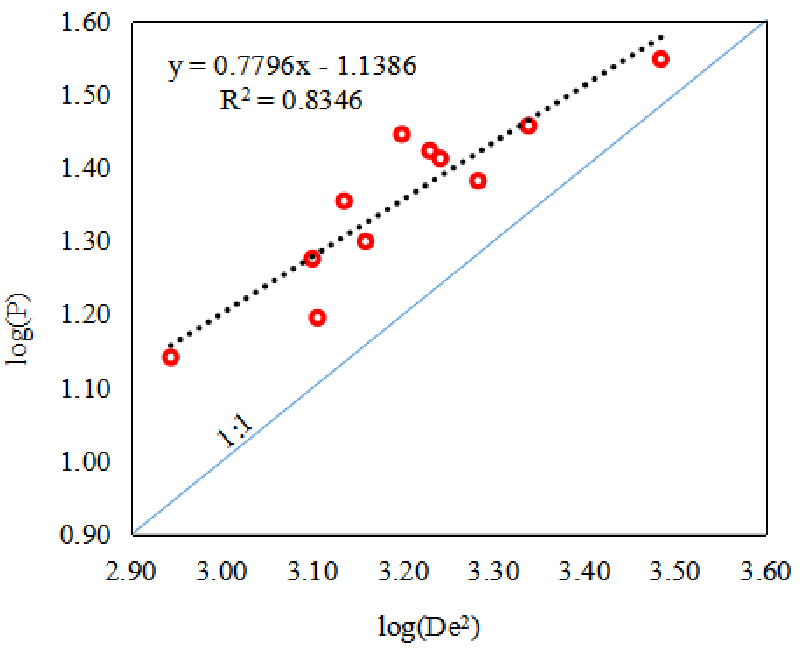
According to the Standard for test methods of engineering rock mass [18], the correction index m = 2(1-n), where n is the slope of the logP-logD²e curve. The logP-logD²e curves of parallel stratification were shown in Figure 4, and the logP-logD²e curves of vertical stratification were shown in Figure 5.

Figure 4: The logP-logD2e curves of parallel stratification.

Figure 5: The logP-logD2e curves of vertical stratification.

The parallel stratification, n = 0.7952, m = 0.4096. The vertical stratification, n = 0.7796, m = 0.4408. The R2 was 0.6223 and 0.8346, respectively, indicating that the correlation for logP and logD2e was pretty. Meanwhile, the correction index was 0.4096 and 0.4408, both between 0.40 and 0.45 [18], indicating the feasibility of the PLT.

The conversion relationship between the I_s(50) and the UCS

SPSS 26.0 was adopted to analyze the data of I_s(50) and UCS, and the least square regression method was employed for I_s(50) - UCS fitting. Firstly, assume that $w(x_i)$ is a weight function, $\text{y}=f(x,\overrightarrow{\beta })$ as a fitting function, determine $\overrightarrow{\beta }={\overrightarrow{\beta }}^{*}$ , so that (Eq. 6-7):

${\displaystyle \sum _{i=1}^{n}w(x_i)}{[y_i-f(x_i,{\overrightarrow{\beta }}^{*})]}^2=\underset{\beta }{\min }{\displaystyle \sum _{i=1}^{n}w(x_i)}{[y_i-f(x_i,\overrightarrow{\beta })]}^2\text{ (6)}$

$\frac{\partial }{\partial \overrightarrow{\beta }}{\displaystyle \sum _{i=1}^{\text{n}}w(x_i)}{[y_i-f(x_i,\overrightarrow{\beta })]}^2|{}_{\overrightarrow{\beta }={\overrightarrow{\beta }}^{*}}=0\text{ (7)}$

fitting function can be obtained.

R² is used to evaluate both the advantages and disadvantages of the model, i.e. the percentage of the regression squares’ sum in the total squares’ sum, as shown in Eq. 8.

${\text{R}}^2=\frac{S{S}_{\text{Regression}}}{S{S}_{\text{Total}}}\text{ (8)}$

The value range of R² is 0≤R²≤1. The closer R² is to 1, that is, the better the sample data fit the selected model, the higher the goodness of fit of the model. The statistical quantity can reflect the extent to which the model explains the variability of the dependent variable, and can also be interpreted as the percentage of the total variation of the dependent variable reduced by the regression Equation. The hypothesis test on the goodness of fit of the regression Equation based on the determination coefficient R² is completely equivalent to the analysis of variance of the entire regression Equation. See Eq. 9 for the calculation.

$\text{F}=\frac{{\text{SS}}_{\text{Regression}}/p}{SS{}_{\text{Residual}}/(n-p-1)}=\frac{R^2/p}{(1-{\text{R}}^2)/(n-p-1)}\text{ (9)}$

Where p is the number of independent variables in the model and n is the sample size.

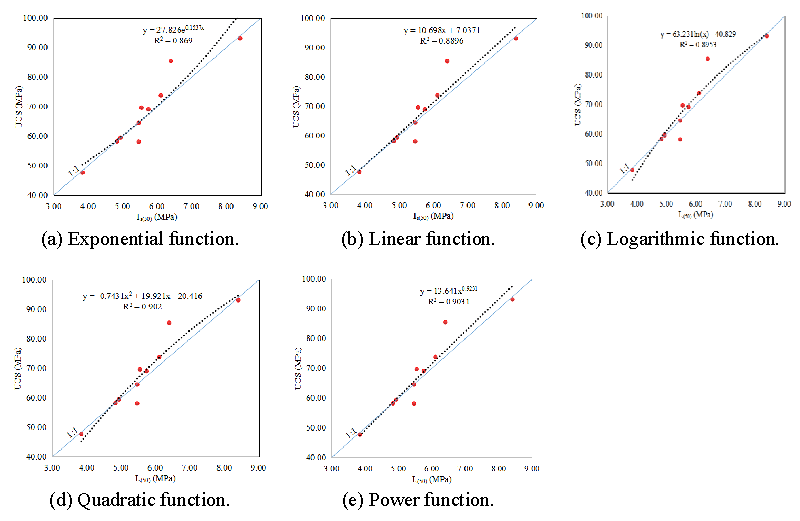
The conversion relationship between the I_s(50) and the UCS for parallel stratification: The conversion relationship of I_s(50) and UCS for parallel stratification is shown in Figure 6.

Figure 6: The functional relationship of I_s(50) and UCS for parallel stratification.

The R2 of exponential, linear, logarithmic, quadratic, and power functions is between 0.869 - 0.9031, indicating that the correlation for I_s(50) and UCS was pretty. The closer R2 is near to 1, the higher the fitness is. Combining the inherent properties of the rock itself, the power function between I_s(50) and UCS was selected as the conversion relationship for the parallel stratification (Figure 6).

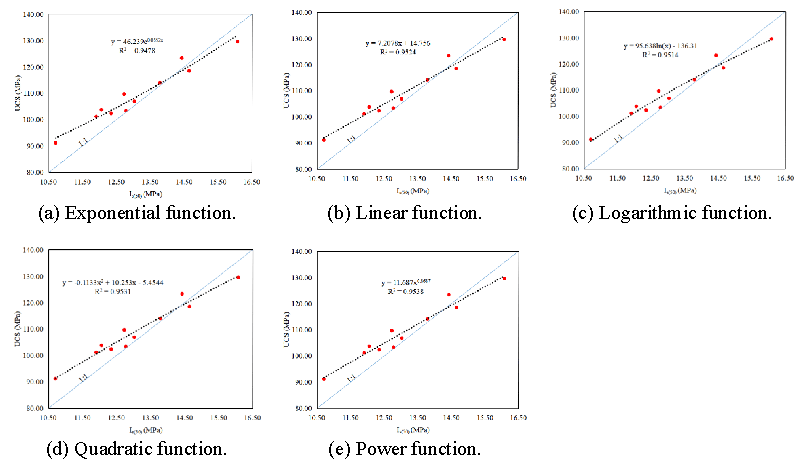
The conversion relationship between the I_s(50) and the UCS for vertical stratification: The conversion relationship of I_s(50) and UCS for vertical stratification is shown in Figure 7.

The R2 of exponential, linear, logarithmic, quadratic, and power functions is between 0.9478 - 0.9538, indicating that the correlation for I_s(50) and UCS was pretty. The closer R2 is near to 1, the higher the fitness is. Combining the inherent properties of the rock itself, the power function between I_s(50) and UCS was selected as the conversion relationship for the vertical stratification (Figure 7).

Figure 7: The functional relationship of I_s(50) and UCS for vertical stratification.

Comparison analysis with the other researchers’ study

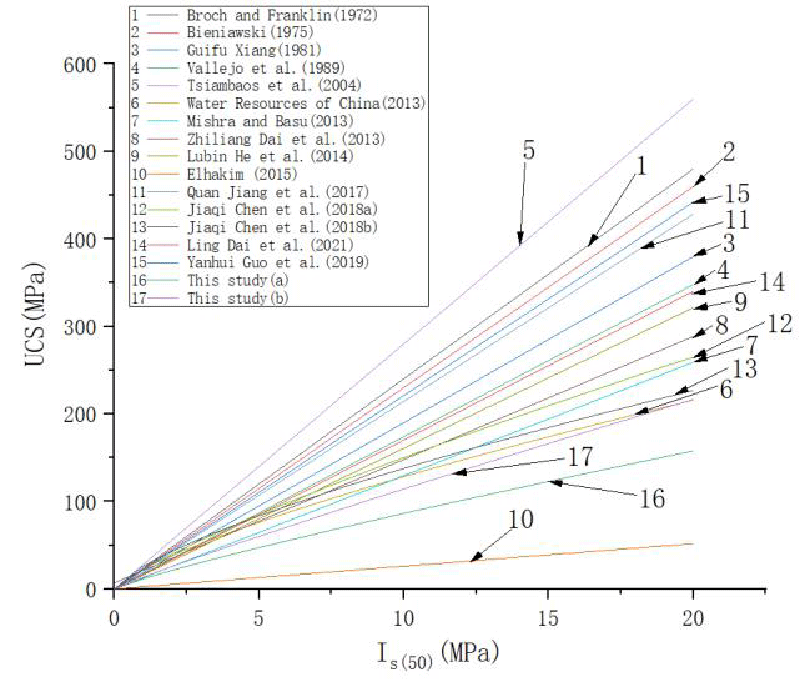
Combined with the previous research results about the fitting function between I_s(50) and UCS of the red sandstone, the UCS calculated by using I_s(50) from different researchers are compared, and the results of the comparison was shown in Figure 8.

Parallel stratification’s I_s(50) is between 3.84 - 8.41 MPa, and vertical stratification’s I_s(50) is between 10.71 - 16.08 MPa. According to the I_s(50) and UCS conversion obtained in Figure 8, both parallel stratification and vertical stratification are basically consistent with Chen’s results [24] (a) rule shape and standard [18], indicating that the power function relationship between I_s(50) and UCS of red sandstone is of great guiding significance.

Figure 8: The comparison of the conversion relationship between I_s(50) and UCS from different researchers.

Conclusion

In summary, the red sandstone of Xiaopu 3# branch Cave in Yuxi section of the CYWD Project was taken as the research object. The UCS and PLT are conducted from the perspectives of vertical and parallel stratifications, respectively. The effect of correction index m on calculating red sandstone strength parameters was analyzed and discussed, and the main conclusions are as follows:

• The mechanical properties of red sandstone had obvious anisotropy.
• PLT is utilized to determine the degree of anisotropy of the rock. The anisotropy index of the red sandstone is b = 2.31.
• The point load strength correction index m of red sandstone is m = 0.4096 under parallel stratification and m = 0.4408 under vertical stratification.
• The conversion relationship between I_s(50) and UCS is a power function under both parallel stratification and vertical stratification.

This study exclusively focused on the uniaxial compressive strength analysis of red sandstone, without investigating the examination of its stress-strain relationship under triaxial test conditions. Moreover, this research specifically concentrated on the red sandstone found in Yuxi section of the CYWD Project, leaving the comprehensive exploration of red sandstone’s diverse physical and mechanical properties on a broader scope as a subject for future investigation.

The authors gratefully acknowledge the support provided by the National Natural Science Foundation of China (11762009, 12162017), the Analysis and Testing Foundation of Kunming University of Science and Technology (2022P20201110007), and the Basic Research Project of Yunnan Province (202101AU070032).

The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

1. Jalali SH. Predicting of uniaxial compressive strength of some igneous and metamorphic rocks by block punch index and cylindrical punch index tests, International Journal of Rock Mechanics and Mining Sciences. 2019; 119:72-80.
2. Jamshidi A. A Comparative Study of Point Load Index Test Procedures in Predicting the Uniaxial Compressive Strength of Sandstones, Rock Mechanics and Rock Engineering. 2022; 55:7; 4507-4516.
3. Liu Q, Zhao Y, Zhang X. Case study: using the point load test to estimate rock strength of tunnels constructed by a tunnel boring machine, Bulletin of Engineering Geology and the Environment. 2017; 78: 3; 1727-1734.
4. Kumsar H. Dynamic and Static Stability Assessment of Rock Slopes Against Wedge Failures, Rock Mechanics and Rock Engineering. 2000; 33: 1; 31-51.
5. Yu C. The effect of water on the creep behavior of red sandstone. Engineering Geology. 2019; 253,:64-74; 2019/04/10/.
6. Singh TN, Kainthola A, Venkatesh A. Correlation Between Point Load Index and Uniaxial Compressive Strength for Different Rock Types,” Rock Mechanics and Rock Engineering. 2012; 45:2; 259-264.
7. Garrido ME. Predicting the Uniaxial Compressive Strength of a Limestone Exposed to High Temperatures by Point Load and Leeb Rebound Hardness Testing. Rock Mechanics and Rock Engineering. 2022; 55:1; 1-17.
8. Ng IT, Yuen KV, Lau HC. Predictive model for uniaxial compressive strength for Grade III granitic rocks from Macao. Engineering Geology. 2015; 199:28-37,.
9. ISRM. Rock characterization, testing & monitoring: ISRM suggested methods: Pergamon Press, Oxford. 1981.
10. ASTM. Standard test method of unconfined compressive strength of intact rock core specimens, ASTM Publication. 1986.
11. Wang M. Summary of the Transformational Relationship between Point Load Strength Index and Uniaxial Compressive Strength of Rocks, Sustainability. 2022; 14:19.
12. Kong F, Shang J. A Validation Study for the Estimation of Uniaxial Compressive Strength Based on Index Tests,” Rock Mechanics and Rock Engineering. 2018; 51: 7; 2289-2297.
13. Şahin M, Ulusay R, Karakul H. Point Load Strength Index of Half-Cut Core Specimens and Correlation with Uniaxial Compressive Strength, Rock Mechanics and Rock Engineering. 2020; 53: 8; 3745-3760.
14. Xie W. Experimental investigation of rock strength using indentation test and point load test,” International Journal of Rock Mechanics and Mining Sciences. 2021; 139.
15. Protodyakonov M. New methods of determining mechanical properties of rock. 187-195.
16. D'Andrea DV, Fischer RL, Fogelson DE. Prediction of compressive strength from other rock properties: US Department of the Interior, Bureau of Mines. 1964.
17. ISRM. Suggested method for determining point load strength,” International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1985; 22: 2; 51-60.
18. Broch E, Franklin JA. The point-load strength test,” International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1972; 9:6; 669-676.
19. Bieniawski ZT. The point-load test in geotechnical practice. Engineering Geology. 1975; 9:1; 1-11.
20. Xiang GF. Comparative Study of Point Load test on rock, " Hydrogeology and engineering geology. 1981; 41-45.
21. Vallejo LE, Welsh RA, Robinson MK. Correlation between unconfined compressive and point load strengths for Appalachian rocks.
22. Tsiambaos G, Sabatakakis N. Considerations on strength of intact sedimentary rocks, Engineering Geology. 2004; 72:3-4; 261-273.
23. Ministry of Housing and Urban-Rural Development of the People's Republic of China, Standard for test methods of engineering rock mass ( GB/T 50266 - 2013), Beijing: China Planning Press. 2013.
24. Mishra DA, Basu A. Estimation of uniaxial compressive strength of rock materials by index tests using regression analysis and fuzzy inference system. Engineering Geology. 2013; 160:54-68.
25. Fu ZL, Wang L. Comparative experimental research on point load strength, uniaxial compressive strength and tensile strength for rocks in roof and floor of coal seam. Chinese Journal of Rock Mechanics and Engineering.2013; 32(1):88-97.
26. He LB, Fu ZL, Wang Q. Linear relationship between point load strength and uniaxial compressive strength of rock. Coal geology and exploration. 2014; 42(3),:68-73.
27. [27]  A. F. Elhakim, “The use of point load test for Dubai weak calcareous sandstones,” Journal of Rock Mechanics and Geotechnical Engineering, vol. 7, no. 4, pp. 452-457, 2015.
28. Jiang Q, Cui J, Feng XT. Stochastic statistics and probability distribution estimation of mechanical parameters of basalt. Rock and Soil Mechanics. 2017; 38(3):784-792.
29. Chen JQ, Wei ZA. Comparison of rock strength from different point load tests and the uniaxial compressive strength. The Chinese Journal of Geological Hazard and Control. 2018; 29(5):72-77.
30. Dai L, Yao HY, Zhang FY. Experimental study on point load strength of red sandstone with different shapes. Science Technology and Engineering. 2019L; 34(5):13-17.
31. Guo YH, Hou KP, Jiang J. Study on the Relationship Between Point Load Strength and Uniaxial Compressive Strength of Several Rocks. China Tungsten Industry. 2019; 19(7):209-214.
32. Dai L, Yao HY, Pan PZ. Point Load Test and Analysis of Disc Rocks with Different Diameters. Water Resources and Powe.2021; 39(5):147-150.
33. Wong RHC. Uniaxial compressive strength and point load index of volcanic irregular lumps. International Journal of Rock Mechanics and Mining Sciences.2017; 93:307-315.
34. Yin JH. Point load strength index of granitic irregular lumps: Size correction and correlation with uniaxial compressive strength. Tunnelling And Underground Space Technology. 2017; 70:388-399.
35. Li HP, Wu YY, Ge C. The relation between point load strength and compressive and tensile strength of marble. Science Technology and Engineering. 2019; 19(32):294-299.
36. Yao JL, Yao HY, Dai L. Study on the Mechanical Characteristics of Anisotropic Gneiss under Point Load and Uniaxial Compression. Chinese Journal of Underground Space and Engineering. 2021; 17(4):1038-1044.
37. Tang S. The effects of water on the strength of black sandstone in a brittle regime. Engineering Geology. 2018; 239:167-178.
38. Wang M. Study on Construction and Reinforcement Technology of Dolomite Sanding Tunnel. Sustainability. 2022; 14:15.
39. ISRM. The complete ISRM suggested methods for rock characterization, testing, and monitoring: 1974-2006. In: Ulusay, R., Hudson, J.A. (Eds.), Suggested Methods Prepared by the Commission on Testing Methods. Compilation Arranged by the ISRM Turkish National Group. International Society for Rock Mechanics. Ankara. Turkey. 2007.
40. ASTM. Standard test methods for compressive strength and elastic moduli of intact rock core specimens under varying states of stress and temperatures: D7012–14. Annual book of ASTM standards. 2014.
41. ASTM. Standard Practices for Preparing Rock Core Specimens and Determining. 2001.